This is my blog.

为什么要研究视觉？

计算机视觉：从图像或图像序列中获取对世界的描述
从运动求取结构技术：从图像序列中获取所见物体的描述以及摄像机的运动规律
医学图像处理与理解；检验人们对物体拍摄的图像，以便确定它们是否符合规定；卫星图像的理解；对收集的图片加以组织与结构化

第一章摄像机

针孔摄像机

透视投影

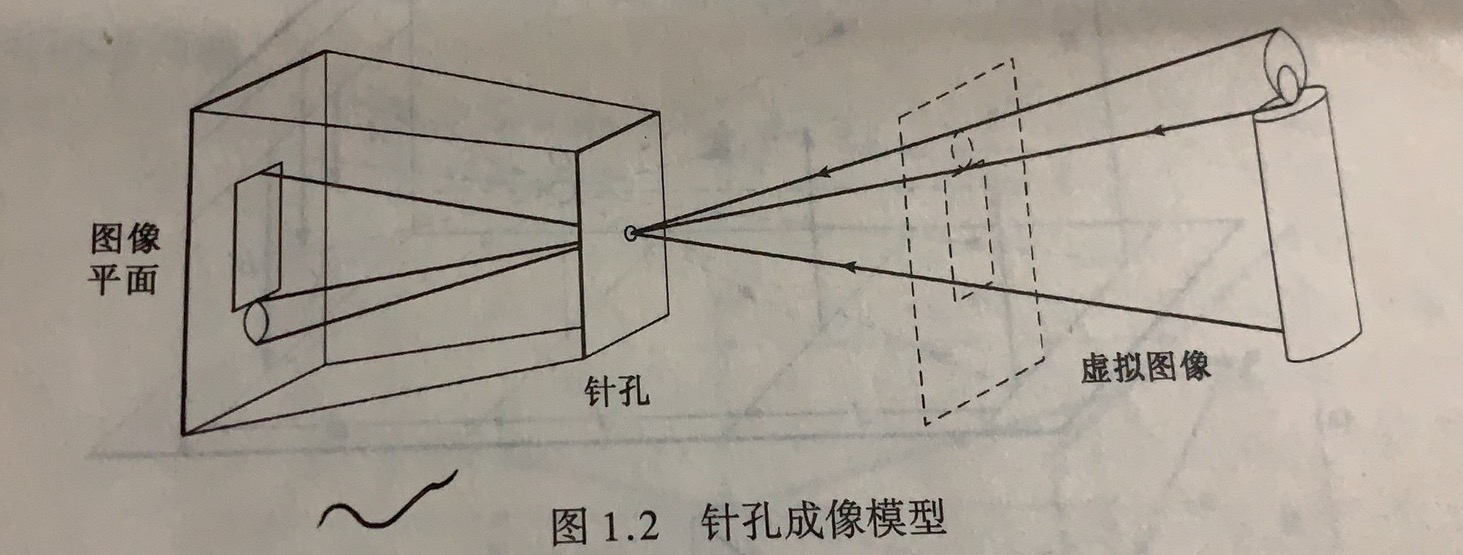
针孔成像模型

下图表明了透视投影的效果：所观察到的物体大小取决于它们的距离

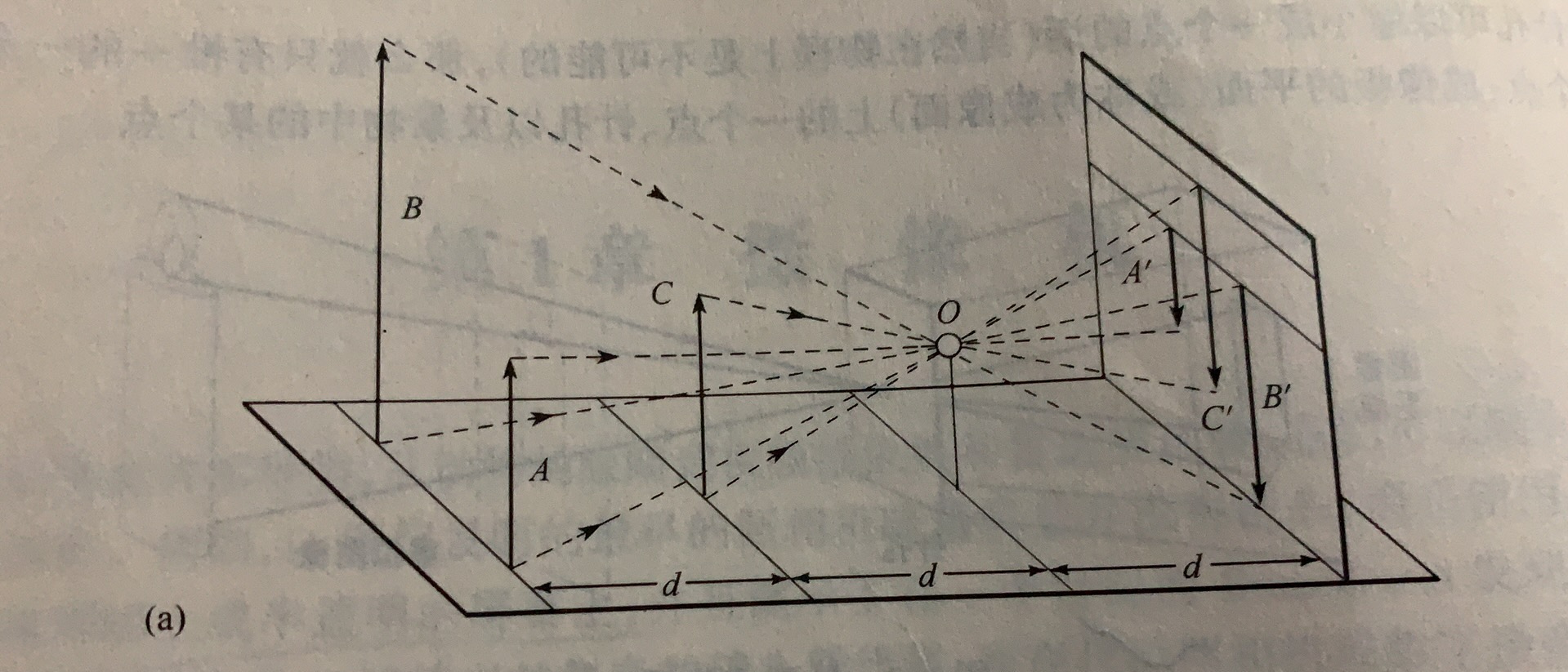
下图表明了：同一平面II上的两条平行线的投影在成像面上将会聚到（成像面上）一条水平线H上，H这条线是穿过针孔与II平行的平面与成像面相交的交线【同时，平面II上与成像面平行的线L在成像面上没有图像】

透视投影方程式

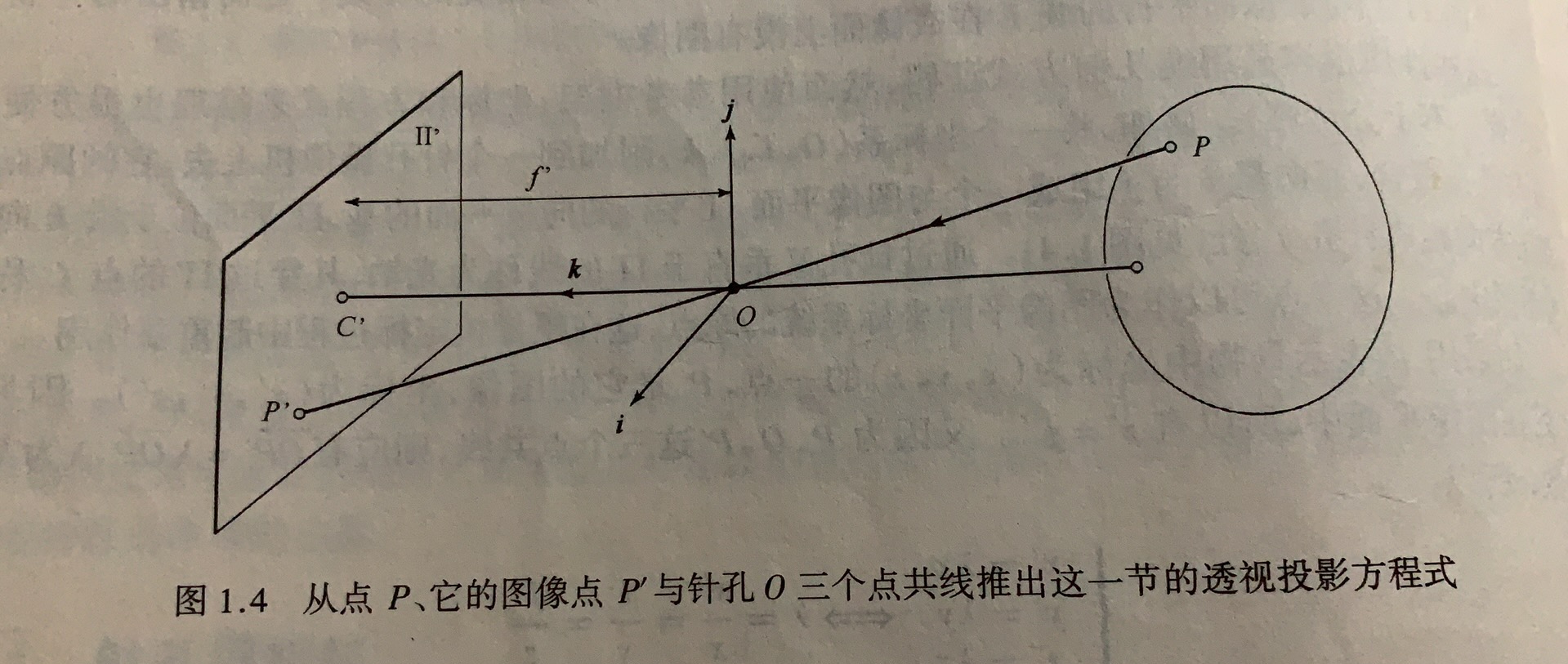
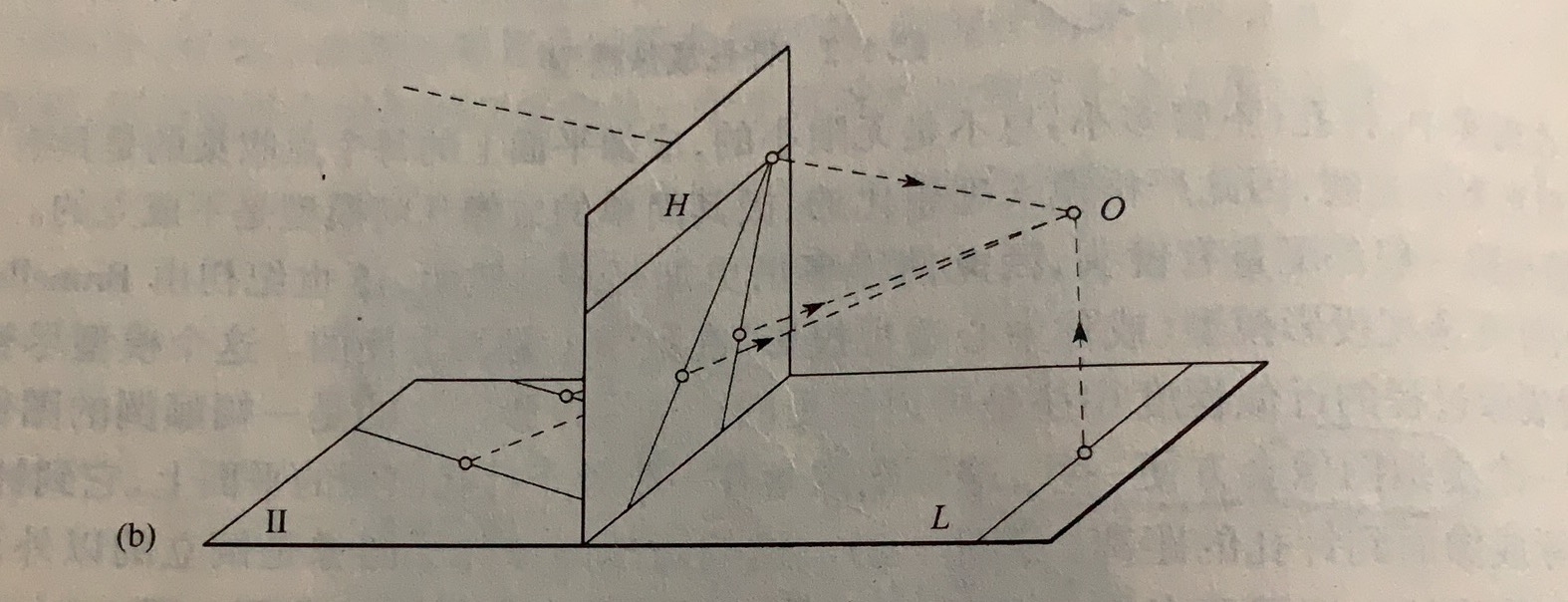
图中，点$P$表示景物中坐标为$(x,y,z)$的一点，$P’$是它的图像，坐标为$(x’,y’,z’)$。因为P’处在图像中，所以有$z’=f$，又因为$P$，$O$，$P’$三点共线，则有：

$\begin{cases}x'=\lambda x\\y'=\lambda y\\f' = \lambda z \end{cases}\Leftrightarrow \lambda=\frac{x'}{x}=\frac{y'}{y}=\frac{z'}{z}$

因此有

$\begin{cases}x'=f'\frac{x}{z} \\ y'=f'\frac{y}{z}\end{cases}$

其中$x,y$是世界坐标，$x’, y’$是图像坐标，$f’$是针孔到视网膜的距离

仿射投影

以上面图a来说明，$z$必定为负值，因为平面位于针孔的前面。且m是个正值，称为放大率。当景物深度与它们到摄像机的平均距离相比很小时，m可以看作是一个常数，这种投影模型称为弱透视模型或按比例的正交。

弱透视投影：

$\begin{cases}x'=-mx \\ y'=-my\\m=-\frac {f'}{z_0}\end{cases}$

其中$z_0$参考点深度（$<0$），$m$放大倍数（$>0$）

当$m=-1$时，这就是正交投影，可以想象一下，满足这种条件的时候，光都是平行的。

$\begin{cases}x'=x \\ y'=y\end{cases}$

带镜头的摄像机

使用镜头的理由：保持图像锐化聚焦，同时又可以从大面积中收集光线

折射公式Snell规则

$n_1\text{sin}\ \alpha_1=n_2\text{sin}\ \alpha_2$

其中$n$是折射率，$\alpha$到法线的夹角

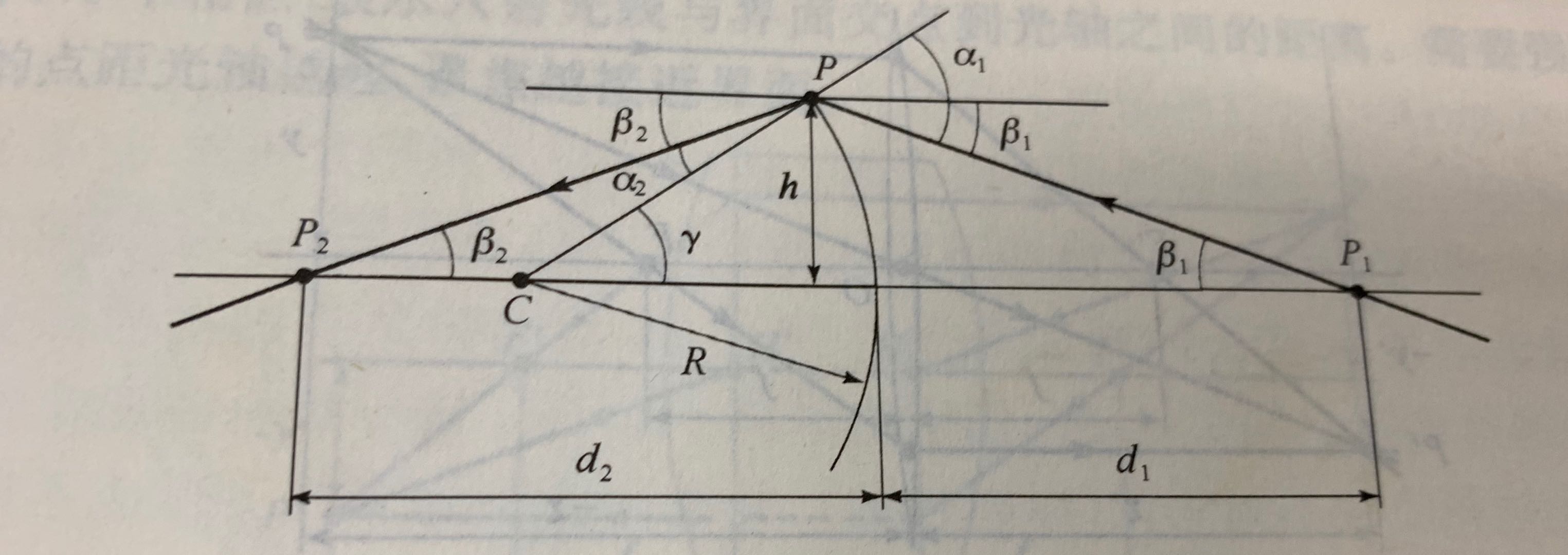
近轴折射方程式

$n_1\alpha_1\approx n_2\alpha_a\Leftrightarrow \frac{n_1}{d_1}+\frac{n_2}{d_2}=\frac{n_2-n_1}{R}$

推导成右式需要再增加角度的关系，以及由于角度较小用正切或正弦值代替，即$\alpha_1=\gamma+\beta_1\approx h(\frac1 R+\frac 1 {d_1})$和$\alpha_2=\gamma+\beta_2\approx h(\frac1 R-\frac 1 {d_2})$

薄透镜方程

$\frac 1 {z'}-\frac 1 z=\frac 1 f$

其中，$z$物点深度（$<0$），$z’$像点深度（$>0$）$f$焦距

第二章摄像机的几何模型

欧几里得解析几何基础

右手坐标系，$i,j,k$分别对应右手的手指，拇指向上，食指向前，中指向左

齐次坐标可以表示点、向量、平面；若要转换成普通坐标，只需要同除以最后一项即可

原点不同，移动$\sideset{^B}{}P = \sideset{^A}{}P+\sideset{^B}{}O_A$；基向量不同，旋转$\sideset{^B}{}P = \sideset{^B_A}{^A}RP$；一般的刚体变换，$\sideset{^B}{}P = \sideset{^B_A}{^A}RP+\sideset{^B}{_A}O$，写成矩阵的形式$\left(\begin{matrix}\sideset{^B}{}P\\1\end{matrix}\right)=\sideset{^B_A}{}{\cal{T}}\left(\begin{matrix}\sideset{^A}{}P\\1\end{matrix}\right)$，其中，$\sideset{^B_A}{}{\cal{T}}=^\text{def}\left(\begin{matrix}\ \sideset{^B_A}{^A}RP& \ \sideset{^B}{_A}O\\0^T& 1\end{matrix}\right)$

若R是一个非奇异3x3矩阵，则称$\cal{T}$表示一个仿射变换，新的坐标轴不一定能保证坐标轴长度为1且正交；若$\cal{T}$是非奇异4x4矩阵，则称其为投影变换

在坐标变换中，下标表示被表示的对象，而上标指示用来表示对象的坐标系

旋转矩阵的特点：

旋转矩阵的逆矩阵和它的转置相同
旋转矩阵的模是1
一个旋转的各列构成了右手正交坐标系
两个旋转矩阵的乘积仍然是旋转矩阵
旋转矩阵的乘法满足结合律

摄像机参数和透视投影

内参数

$\begin{cases}u=\alpha\frac x z-\alpha\text{cot}\theta\frac y z+u_0\\v=\frac \beta {\text{sin}\theta}\frac y z+v_0\end{cases}$ $p=\left(\begin{matrix}u\\v\\1\end{matrix}\right), \cal{K}=^\text{def}\left(\begin{matrix}\alpha & -\alpha\text{cot}\theta & u_0\\0&\frac \beta{\text{sin}\theta} & v_0\\0& 0& 1\end{matrix}\right)\\p=\frac 1 z\cal{M}p, \cal{M}=^\text{def}\left(\begin{matrix}\cal{K} & 0\end{matrix}\right)$

用$a^T_i(i=1,2,3)$表示由$\cal{A}$的最左边3列构成的矩阵$\cal{M}$的各行

$\cal{K}$内参数矩阵，透视投影矩阵$\cal{M}=\cal{K}(R\ t)$

$\cal{M}$是透视投影矩阵的充要条件是$Det(A)\not=0$

$\cal{M}$是无偏歪透视投影矩阵的充要条件是$Det(A)\not=0$且$(a_1\times a_3)\cdot (a_2\times a_3)=0$

$\cal{M}$是无偏歪单位长宽比透视投影矩阵的充要条件是$Det(A)\not=0$且$\begin{cases}(a_1\times a_3)\cdot (a_2\times a_3)=0\(a_1\times a_3)\cdot(a_1\times a_3)=(a_2\times a_3)\cdot(a_2\times a_3)\end{cases}$

外参数

$\left(\begin{matrix}\sideset{^C}{}P\\1\end{matrix}\right)=\left(\begin{matrix}\ \sideset{^C_W}{}R& \ \sideset{^C}{_W}O\\0^T& 1\end{matrix}\right)\left(\begin{matrix}\sideset{^W}{}P\\1\end{matrix}\right)$

光心是唯一一个图像不唯一确定的点，满足$\cal{M}\bf{0}=0$

投影矩阵可以由5个内参数和6个外参数（三个表示R，三个表示t）显式表达

仿射摄像机

当场景的深度大小变化远小于场景距摄像机的距离时，可以用仿射投影近似成像过程。

~~近不下来看下次补~~

仿射投影方程 $p=\cal{M}\left(\begin{matrix}P\\1\end{matrix}\right)=AP+b$

弱透视投影矩阵 $\cal{M}=(A \ b)=\frac 1 {z_r}\left(\begin{matrix}k&s\\0& 1\end{matrix}\right)\left(\begin{matrix}\cal{R}_2 &t_2\end{matrix}\right)$

类透视投影矩阵I $\cal{M}=\frac 1 {z_r}\left(\begin{matrix}k&s\\0& 1\end{matrix}\right)\left(\begin{matrix}\left(\begin{matrix}1&0&-x_r/z_r\\0&1&-y_r/z_r\end{matrix}\right)\cal{R} &t_2\end{matrix}\right)$

类透视投影矩阵II $\cal{M}=\frac 1 {z_r}\left(\begin{matrix}\left(\begin{matrix}k&s&u_0-u_r\\0&1&v_0-v_r\end{matrix}\right)\cal{R} &\left(\begin{matrix}k&s\\0& 1\end{matrix}\right)t_2\end{matrix}\right)$

三个几何问题

From 《计算机视觉模型、学习、推理》

前景：$x=pinhole[w,K,R,T]$

$Pr(x|w,A,R,T)=Norm_x[pinhole[w,K,R,T],\sigma^2I]$

其中$\sigma^2$是噪声方差，加性噪声通常以球形协方差分布

学习外在参数

假设一个已知对象有I个不同的3D点$\{w_i\}^{I}_{i=1}$，他们在图像中的对应投影点为$\{x_i\}^I_{i=1}$，以及已知的内在参数$K$。目标是对旋转矩阵$R$和平移矢量$T$进行估计，这两者可以将目标坐标系中的点映射为摄像机坐标系中的点，使得

$\hat{R},\hat{T}=\displaystyle argmax_{R,T}[\sum^I_{i=1}log[Pr(x_i|w_i,K,R,T)]]$

这是最大似然学习问题，我们的目标是要找到参数$R$和$T$使得模型的预测$pinhole[w_i,K,R,T]$与观测的2D点$x_i$一致

我们已知

$\lambda z_c\left(\begin{matrix}x\\y\\1\end{matrix}\right)=\left(\begin{matrix}w_{11} & w_{12}&w_{13}&t_x\\w_{21} & w_{22}&w_{3}&t_y\\w_{31} & w_{32}&w_{33}&t_z\end{matrix}\right)\left(\begin{matrix}x_w\\y_w\\z_w\\1\end{matrix}\right)$

易得

$\lambda = w_{31}x_w+w_{32}y_w+w_{33}z_w+t_z$

将上式带入矩阵，可得

$\left(\begin{matrix}(w_{31}x_w+w_{32}y_w+w_{33}z_w+t_z)x\\(w_{31}x_w+w_{32}y_w+w_{33}z_w+t_z)y\end{matrix}\right)=\left(\begin{matrix}w_{11} & w_{12}&w_{13}&t_x\\w_{21} & w_{22}&w_{3}&t_y\end{matrix}\right)\left(\begin{matrix}x_w\\y_w\\z_w\\1\end{matrix}\right)$

由此我们可以构建方程组：

$\left(\begin{matrix}x_{w1}&y_{w1}&z_{w1}&1&0&0&0&0&-x_{w1}x_{c1}&-y_{w1}x_{c1}&-z_{w1}x_{c1}&-x_{c1}\\ 0&0&0&0&x_{w1}&y_{w1}&z_{w1}&1&-x_{w1}y_{c1}&-y_{w1}y_{c1}&-z_{w1}y_{c1}&-y_{c1}\\ x_{w2}&y_{w2}&z_{w2}&1&0&0&0&0&-x_{w2}x_{c2}&-y_{w2}x_{c2}&-z_{w2}x_{c2}&-x_{c2}\\ 0&0&0&0&x_{w2}&y_{w2}&z_{w2}&1&-x_{w2}y_{c2}&-y_{w2}y_{c2}&-z_{w2}y_{c2}&-y_{c2}\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ x_{wI}&y_{wI}&z_{wI}&1&0&0&0&0&-x_{wI}x_{cI}&-y_{wI}x_{cI}&-z_{wI}x_{cI}&-x_{cI}\\ 0&0&0&0&x_{wI}&y_{wI}&z_{wI}&1&-x_{wI}y_{cI}&-y_{wI}y_{cI}&-z_{wI}y_{cI}&-y_{cI}\\ \end{matrix}\right)\left(\begin{matrix}w_{11}\\w_{12}\\w_{13}\\t_x\\w_{21}\\w_{22}\\w_{23}\\t_y\\w_{31}\\w_{32}\\w_{33}\\t_z\end{matrix}\right)=0$

这样问题变为了求解最小方向问题（类似于椭圆中找到主轴）的标准形式$Ab=0$，我们要在满足$|b|=1$的条件下，寻找使$|Ab|^2$最小的b值，可以通过计算奇异值分解$A=ULV^T$并将$\hat b$设置为V的最后一列来得到解

学习内在参数

目标是对内在参数$K$进行估计，$K$将通过光心的光线方向与图像平面上的坐标相关联。这一估计过程称为校准。

形式化描述：给定一个已知3D对象，该对象有I个不同的3D点$\{w_i\}^{I}_{i=1}$以及在图像中的对应投影点$\{x_i\}^I_{i=1}$，对内在参数估计

$\hat{K}=argmax_{K}[max_{R,T}[\displaystyle\sum^I_{i=1}log[Pr(x_i|w_i,K,R,T)]]]$

这是最大似然学习问题，我们的目标是要找到参数$K, R$和$T$使得模型的预测$pinhole[w_i,K,R,T]$与观测的2D点$x_i$一致

推理3D世界点

给定$2\leq J$个校准摄像机以及场景中的点$w$在其中的投影$\{x_j\}^I_{J=1}$，我们希望对点$w$的3D位置进行估计

当$j=2$时，称为校准立体重构；当$J>2$时，这称为多视图重构

形式化描述：在已知位置有$J$个校准摄像机对同一个3D点$w$进行观测，且已知对应的2D投影$\{x_j\}^I_{J=1}$，则在$J$幅图像中可以建立现实世界中点的3D位置$w$

$\hat{w}=argmax_{w}[\sum^J_{j=1}log[Pr(x_j|w,K_j,R_j,T_j)]$

第三章摄像机的几何标定

摄像机标定可以看做是一个优化问题，优化的目标是使摄像机观察到的特征与理论位置之间的距离最小

径向畸变

由于目标点偏离光轴而引起的畸变；改变了图像点p到图像中心的距离，但是没有改变图像点相对于中心直线方向；当$8\leq n$时，可以用齐次线性最小二乘法计算单位向量m的值

$\cal{Q}=^\text{def}\left(\begin{matrix}v_1P_1^T&-u_1P_1^T\\\cdot\cdot\cdot&\cdot\cdot\cdot&\cdot\cdot\cdot\\v_nP_n^T&-u_nP_n^T\end{matrix}\right),n=^\text{def}\left(\begin{matrix}m_1\\m_2\end{matrix}\right)$

估计内外参数：

$\frac \beta \alpha=\frac {|a_2|}{|a_1|},cos\theta=-\frac{a_1\cdot a_2}{|a_2||a_1|}$

$\alpha=\epsilon p|a_1|sin\theta, \beta=\epsilon p|a_2|sin\theta, \epsilon=\pm1$

$\begin{cases}r_1=\frac \epsilon{sin\theta}(\frac 1 {|a_1|}+\frac {cos\theta}{|a_2|})\\r_2=\frac \epsilon{a_2}a_2\\r_3=r_1r_2\end{cases}$

$\left(\begin{matrix}\alpha_x-\alpha cot\theta t_y\\\frac \beta {sin\theta}t\end{matrix}\right)=p\left(\begin{matrix}b_1\\b_2\end{matrix}\right)$

最小二乘法的参数估计

最小二乘法的意思就是使均方误差最小化

线性最小二乘法

假设有p个关于q个未知数的线性方程组，则

当$p<q$时，方程的解集构成一个(q-p)维的$\R^q$上的子空间

当$p=q$时，有唯一的解

当$p>q$时，方程无解

当方程组的右侧均为0的时候，则是齐次系统了

非线性最小二乘法

当$p<q$时，解构成一个$\R^q$上的(q-p)维的子集

当$p=q$时，有有限个解

当$p>q$时，无解

牛顿法、高斯牛顿法（需要复习数值分析部分！！！还没看）

线性方法进行标定

步骤：

计算这个坐标系下摄像机的投影矩阵$\cal{M}$

n个点的约束可以写成2n维的线性方程$\cal{M},Pm=0$，方程参数为投影矩阵的分量
$\cal{P}=^\text{def}\left(\begin{matrix}P_1^T&0^T&-u_1P_1^T\\0^T&P_1^T&-v_1P_1^T\\\cdot\cdot\cdot&\cdot\cdot\cdot&\cdot\cdot\cdot\\P_n^T&0^T&-u_nP_n^T\\0^T&P_n^T&-v_nP_n^T\end{matrix}\right),m=^\text{def}\left(\begin{matrix}m_1\\m_2\\m_3\end{matrix}\right)$
当$6\leq n$时，可以用齐次线性最小二乘法计算单位向量m的值
从投影矩阵估计摄像机的内外参数（投影矩阵有11个变量，因此根据上述所需的线性约束应该小于等于11）
$\rho(A\ b)=\cal{K}(R\ t)\Leftrightarrow\rho\left(\begin{matrix}a_1^T\\a_2^T\\a_3^T\end{matrix}\right)=\left(\begin{matrix}\alpha r_1^T-\alpha cot\theta r_2^T+u_0r_3^T\\\frac\beta{sin\theta}r_2^T+v_0r_3^T\\r_3^T\end{matrix}\right)$
其中$\rho$是比例系数，使投影矩阵的模为1；若加上旋转矩阵各行都是单位长度且相互垂直的约束，又可以得到
$\begin{cases}\rho=\epsilon/|a_3|\\r_3=\rho a_3\\u_0=\rho^2(a_1\cdot a_3)\\v_0=\rho^2(a_2\cdot a_3)\end{cases} \ \ \epsilon = \mp1$
由于$\theta$取值在$\pi/2$的领域之间，其正弦值总是正的，则有
$\begin{cases}\rho^2(a_1\times a_3)=-\alpha r_2-\alpha cot\theta r_1\\\rho^2(a_2\times a_3)=\frac \beta{sin\theta}r_1\end{cases},\begin{cases}\rho^2|a_1\times a_3|=\frac \alpha {sin\theta}\\\rho^2|a_2\times a_3|=\frac {|\beta|}{sin\theta}\end{cases}$
于是
$\begin{cases}cos\theta=-\frac{(a_1\times a_3)\cdot(a_2\times a_3)}{\|a_1\times a_3\|\cdot\|a_2\times a_3\|}\\\alpha=\rho^2\|a_1\times a_3\|sin\theta\\\beta=\rho^2\|a_2\times a_3\|sin\theta\end{cases}\\ r_1=\frac{\rho^2 sin\theta}{\beta}(a_2\times a_3)=\frac{a_2\times a_3}{\|a_2\times a_3\|}\\r_2=r_3\times r_1$

Zhang’s Method

PPT分布讲解

首先，所有点是在一个平面上，因此在世界坐标系中我们可以认为$z_w=0$（采用平面标定模板），从而外参矩阵的第三列对结果无影响。我们可以将外参矩阵第三列和$z_w$同时删去，简化为

$\left(\begin{matrix}u\\v\\1\end{matrix}\right)\sim\left(\begin{matrix}f_x & 0 & c_x\\0&f_y&c_y\\0&0&1\end{matrix}\right)\left(\begin{matrix}r_{11}&r_{12}&t_1\\r_{21}&r_{22}&t_2\\r_{31}&r_{32}&t_3\end{matrix}\right)\left(\begin{matrix}x_w\\y_w\\1\end{matrix}\right)$

令

$H=\left(\begin{matrix}h_1,h_2,h_3\end{matrix}\right)=\left(\begin{matrix}f_x & 0 & c_x\\0&f_y&c_y\\0&0&1\end{matrix}\right)\left(\begin{matrix}r_{11}&r_{12}&t_1\\r_{21}&r_{22}&t_2\\r_{31}&r_{32}&t_3\end{matrix}\right)=K\left(\begin{matrix}r_1,r_2,t\end{matrix}\right)$

则

$r_1=K^{-1}h_1,r_2=K^{-1}h_2$

又由于$\left(\begin{matrix}r_1,r_2,r_3\end{matrix}\right)$三者正交，因此有

$r_1^Tr_2=0,\|r_1\|=\|r_2\|=1$

由上两个等式可得

$h_1^TK^{-T}K^{-1}h_2=0\\h_1^TK^{-T}K^{-1}h_1-h_2^TK^{-T}K^{-1}h_2=0$

设$B=K^{-T}K^{-1}$，易知$B$是对称正矩阵，我们将重复元素去除，定义$b=(b_{11},b_{12},b_{13},b_{22},b_{23},b_{33})$

综合可知

$Vb=0\\V=\left(\begin{matrix}V_{12}^T\\V_{11}^T-V_{22}^T\end{matrix}\right)\\ V_{ij}=(h_{i1}h_{j1},h_{i1}h_{j2}+h_{i2}h_{j1},\cdot\cdot\cdot)$

Find a solution that minimizes the least-squares error

其中，V是一个2n×6的矩阵，b是一个6维向量，所以

当n≥3，可以得到b的唯一解
当n=2，则可以假设扭曲参数γ=0作为额外的约束条件
当n=1，则值能计算两个相机的内参数

对于方程$Vb=0$可以使用SVD求其最小二乘解。对$V^TV$进行SVD分解，其最小特征值对应的特征向量就是$Vb=0$的最小二乘解，从而求得矩阵B。由于这里得到的B的估计值是在相差一个常量因子下得到的，所以有：

$B=\lambda A^{-T}A$

从而可以得到相机的各个内参数：

$\begin{cases}c_x=\gamma c_y/\beta-B_{13}\alpha^2/\lambda\\ c_y=(B_{12}B_{13}-B_{11}B_{23})/(B_{11}B_{22}-B_{12}^2)\\ \alpha=\sqrt{\lambda/B_{11}}\\ \beta=\sqrt{\lambda B_{11}/(B_{11}B_{22}-B_{12}^2)}\\ \gamma = -B_{12}\alpha^2\beta/\lambda\\ \lambda=B_{33}-[B_{13}^2+c_y(B_{12}B_{13}-B_{11}B_{23})]/B_{11}\end{cases}$

为了进一步增加标定结果的可靠性，可以使用最大似然估计(Maximum likelihood estimation)来优化上面估计得到的结果。

对于畸变部分，张的方法如下：

在张氏标定法中只关注了影响较大的径向畸变。

$(u,v)$是理想的无畸变的像素坐标

$(\hat u, \hat v)$是畸变后的像素坐标

$(u_0,v_0)$是相机的主点

$(x,y)$是理想的无畸变的归一化的图像坐标

$(\hat x,\hat y)$是畸变后的归一化的图像坐标

$k_1,k_2$表示径向畸变的系数

由此我们可以写出径向畸变公式：

$\hat x = x+x[k_1(x^2+y^2)+k_2(x^2+y^2)^2]\\ \hat y = y+y[k_1(x^2+y^2)+k_2(x^2+y^2)^2]$

径向畸变的中心和相机的主心是在相同的位置，即

$\hat u = u_0+\alpha\hat x+\gamma \hat y\\ \hat v=v_0+\beta\hat y$

假设$\gamma y=0$，则由上两式可得

$\hat u = u+(u-u_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2]\\ \hat v = v+(v-v_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2]$

现有n幅图像，每幅图像可用点m个，则我们共可以得到2mn个等式，记$Dk=d$作为矩阵形式

则

$k=\left[\begin{matrix}k_1& k_2\end{matrix}\right]^T=(D^TD)^{-1}D^T d$

然后便是利用最大似然估计取得最优解，即使得下述式子最小

$\displaystyle \sum_{i=1}^n\sum_{j=1}^m\|\hat m(K,k_1,k_2,R_i,t_i,M_{ij})-m_{ij}\|^2$

从而解得$k_1,k_2$后，将图像先去畸变，然后再通过上述的方法用图像坐标来估计相机内参数

转载请注明出处，谢谢。

愿我是你的小太阳

第一章 摄像机