Improving Deep Neural Networks

Posted on | In , | Visitors:

This is my blog.

这段时间忙着准备CCF和PAT

唔……其实只有PAT想好好考啦～

一些莫名的bug

继续学习机器学习啦～

Basic

Train/dev/test sets

每个问题，每个输入数据等都会影响超参数的设置

Train set-> hold out cross validation(development set)->test set

他们之间的比例不一定，当数据很大的时候，比例可以相差到99:1:1；当数据小的时候，可能为60:20:20

确保开发集和测试集的数据分布相同

Bias/Variance

通过观察Train set error 和Dev set error

贝叶斯误差来评估error是否正常

  • 高偏差/欠拟合

    • Bigger network
    • Train longer
    • 换种神经网络结构

  • 高方差/过拟合

    • get more data（可以通过对现有数据的变换，比如对图片进行翻转

    • Regularization

      • Early stopping 早停
        • 无法分开解决优化代价函数和防止过拟合问题（正交化）

    • 换种神经网络结构

高偏差和高方差可以同时出现（比如，总体线性，但是又将个别特殊点区分开了的情况）

Normalizing training sets归一化

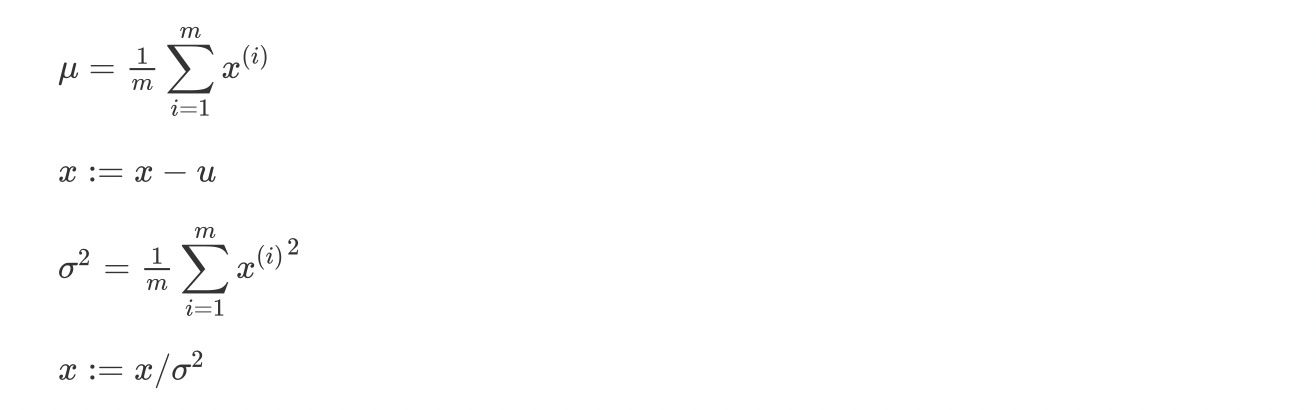
对一个训练集和测试集应该使用相同的归一化参数

如果不归一化，则代价函数的图中是个椭圆，这样在长边的速度就很慢，而如果是个圆，随机初始化后，无论哪个点到最小值的速度都相同，而且到最小值的速度（相对于椭圆，同一个样本中）都很快

Weight initialization

Vanishing/Exploding gradients梯度消失或者爆炸

Gradient checking梯度检验

Mini-batch gradient descent

Hyperparameter：the mini-batch Size

小批量梯度大小的数据大小不可以过大也不可以过小，这样我们可以使用向量的方法，一次处理多个样例

  • Small training set
    • Use batch gradient descent (m<=2000)
  • Typical mini-batch size
    • 64～512设置为2的幂次会快一些
    • 同时size需要可以装进CPU/GPU的容量中

optimization algorithm

Exponentially weighted averages

Bias correction 偏差修正

(gradient descent) Momentum

动量或者动量梯度下降法，几乎比标准的梯度下降法要快

主要思想：计算梯度的指数加权平均，然后使用这个梯度来更新权重

对于不是朝最小值的方向，由于震荡的正负值抵消，所以在其他方向的值在指数加权平均下，震荡的小了；并且在朝最小值的方向上似乎因为动量而加速了

Two Hyperparameter

$\alpha\ and\ \beta $

在动量梯度下降中，不使用偏差修正，因为这里的$\beta$很小，就代表有很多的之前的数据的平均值，已经可以使用了

RMSprop(Root Mean Square prop)

均方根传递算法，可以用来加速梯度下降

目标：减缓不是最小值方向的速度，加快（或者不减慢最小值方向的速度）

Adam optimization algorithm

Hyperparameter

The problem of local optima

局部最优问题

Saddle Point（鞍点）：梯度为0的点，但是在高维空间中，很少出现鞍点是局部最优点的情况（深度学习中一般都是高维空间，有很多参数）

所以降低学习率的不是局部最优问题，而是停滞区

Plateaus（停滞区）：是指导数长时间接近于零的一段区域

可以用Adam等算法，来更快地离开停滞区

Hyperparameter tuning

  • layers

  • hidden units

  • learning rates

  • activation functions

  • mini-batch Size

  • Momentum $\beta$

  • Adam $\beta_1,\beta_2,\epsilon$

  • …

Two ways:

  • Babysitting one model
    • 通常在需要处理一个庞大的数据集，但没有充足的计算资源（CPU/GPU等），所以单个模型，就会细心专注在上面
    • 根据训练情况，逐步更改
  • Training many models in parallel
    • 像鱼产卵一样，一次很多个一起进行，用不同的参数

Some tips:

  • Try random values: don’t use a grid
  • Coarse to fine: 从大体的随机中找到一个小的范围，再进行更密集的随机寻找
  • Using an appropriate scale to pick hyperparameters: 可以不使用线性尺度(linear scale)，而是用对数尺度(log scale)
    • r=(np.log(max)-np.log(min))*np.random.randn()
    • a=np.power(10, r)
    • 因为自变量的变化对值的改变很敏感，所以不用线性了
  • Re-test hyperparameters occasionally：由于数据集的更新，新的机器出现等等，都会导致超参数最优值的变化，所以需要偶尔去重测一下

Algorithm

Batch Normalization批量归一化

在优化算法中的更新参数的部分还是要按优化算法中所说的那样

BN算法，使后面层更加稳定的运算，不太依赖前面的单元，具有一些微弱的正则化的效果（但这不是BN算法的作用，不应该在想要正则化的时候去考虑BN算法）

Multi-class classfication

softmax

在之前的手写数字识别中有提到过，运用在多种(C)分类中

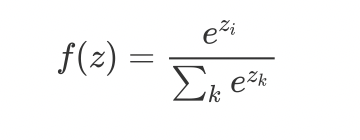
hard max：最大值对应的为1，其余为0的矩阵

Other tips

Epoch Vs Iteration

epoch

当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一次epoch。然而，当一个epoch对于计算机而言太庞大的时候，就需要把它分成多个小块。

Iteration

是batch需要完成一个epoch的次数。

有一个2000个训练样本的数据集。将2000个样本分成大小为500的batch,那么完成一个epoch需要4个iteration。

后记

嚯嚯嚯！出门学习啦～

突然有了不宅在宿舍的动力了

转载请注明出处，谢谢。

愿 我是你的小太阳

买糖果去喽