2018 Multi-University Training hdu Contest 7

Posted on | In , | Visitors:

嚯嚯嚯！补题！

hdu多校总链接

补题： 5题/12题

  • 欧拉函数
  • 莫比乌斯反演
  • LCA
  • RMQ
  • ST
  • 分块
  • 矩阵快速幂
  • IO外挂

A. Age of Moyu

记录每个点当前的最小花费是由哪几种情况转移而来，跑一边迪杰斯特拉就可以了；题解是用set存的，而我这里直接在结构体里多了一个变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
int head[maxn],cnt;
int d[maxn],vis[maxn];
int n,m;
struct Edge{
    int to,nex,id;
}edge[maxn<<2];
struct Node{
    int cost,pre,now;
    Node(int cost_ = 0, int pre_ = 0, int now_ = 0): cost(cost_), pre(pre_), now(now_) {}
    bool operator<(const Node other)const{
        return cost>other.cost;//优先队列，大的在前
    }
}now,temp;
void add(int u,int v,int id){
    edge[++cnt].to=v;
    edge[cnt].nex=head[u];
    edge[cnt].id=id;
    head[u]=cnt;
}
void dijkstra(){
    memset(d,INF,sizeof(d));
    d[1]=0;
    priority_queue<Node>q;
    q.push(Node(0,-1,1));
    int v;
    while(!q.empty()){
        now=q.top();q.pop();
        if(now.cost>d[now.now]) continue;
        for(int i=head[now.now];i;i=edge[i].nex){
            v=edge[i].to;
            temp.now=v;temp.pre=now.pre;temp.cost=now.cost;
            //不用付费
            if(now.pre==edge[i].id&&d[v]>now.cost){
                d[v]=now.cost;
                q.push(temp);
            }
            else if(now.pre!=edge[i].id&&d[v]>now.cost+1){
                d[v] = now.cost + 1;
                temp.cost += 1;
                temp.pre = edge[i].id;
                q.push(temp);
            }
        }
    }
}
int main(){
    while (scanf("%d%d", &n, &m) != EOF) {
        cnt = 0;
        memset(head, 0, sizeof(head));
        int u, v, id;
        for (int i = 1; i <= m; ++i) {
            scanf("%d%d%d", &u, &v, &id);
            add(u, v, id);
            add(v, u, id);
        }
        dijkstra();
        if(d[n]==INF) printf("-1\n");
        else printf("%d\n", d[n]);
    }
    return 0;
}

B. AraBellaC

TLE了

回宿舍，唔，发现下标按顺序的，不用check所有的值，计算每一个的mod len的答案了；直接二分就可以了

题解说的是ST表，不过没想懂mod值不一样，每次都会变化，怎么RMQ呢？

先上一份二分的吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int INF=1e9;
const int maxn=1e4+10;
int a[3][maxn],cnt[3];
int maxx[3],minn[3];
int ans[3];
int n,maxp,x,lena,lenb,lenc;
char c;
bool flag;
int main(){
    int T;scanf("%d",&T);
    while(T--){
        ans[0]=ans[1]=ans[2]=INF;
        memset(cnt,0,sizeof(cnt));
        maxp=0;flag=false;
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            scanf("%d %c",&x,&c);
            a[c-'A'][++cnt[c-'A']]=x;
            maxp=max(maxp,x);
        }
        for(int i=0;i<3;i++){
            a[i][++cnt[i]]=INF;
        }
        for(int len=1;len<=maxp;len++){
            for(int j=0;j<3;j++){maxx[j]=-1;minn[j]=INF;}
            for(int j=0;j<3;j++){
                for(int k=(maxp+len-1)/len;k>0;k--){//第k个循环节
                    x=*(upper_bound(a[j]+1, a[j]+cnt[j]+1, (k-1)*len));
                    if(x<=k*len) minn[j]=min(minn[j],(x-1)%len);
                    x=*(upper_bound(a[j]+1, a[j]+cnt[j]+1, k*len)-1);
                    if(x>(k-1)*len) maxx[j]=max(maxx[j],(x-1)%len);
                    if(maxx[0]>=minn[1]||maxx[1]>=minn[2]) break;
                }
                if(maxx[0]>=minn[1]||maxx[1]>=minn[2]) break;
            }
            if(maxx[0]>=minn[1]||maxx[1]>=minn[2]) continue;
            flag=true;
            lena=maxx[0]+1;lenb=maxx[1]-maxx[0];lenc=len-maxx[1]-1;
            if(lena<ans[0]||(lena==ans[0]&&(lenb<ans[1]||(lenb==ans[1]&&lenc<ans[2])))){
                ans[0]=lena;ans[1]=lenb;ans[2]=lenc;
            }
        }
        if(flag) printf("%d %d %d\n",ans[0],ans[1],ans[2]);
        else printf("NO\n");
    }
    return 0;
}

写完后，现在明白了，我这里找最值是通过每一个循环节中，然后二分答案；而ST表，先预处理区间[l,r]的最值问题，之后，通过固定len枚举每一个循环节，我们可以知道他的左右端点，即可得到这个循环节中的最值了！

代码显而易见，就是把k里东西换成即可

1
2
minn[j]=min(minn[j],RMQ_min((k-1)*len+1,k*len));
maxx[j]=max(maxx[j],RMQ_max((k-1)*len+1,k*len));

ST函数，RMQ函数都是模版的东西，就不放上来了！

E. GuGuFishtion

首先那个函数是欧拉函数哦！

欧拉函数是小于n的正整数中与n互质的数的数目

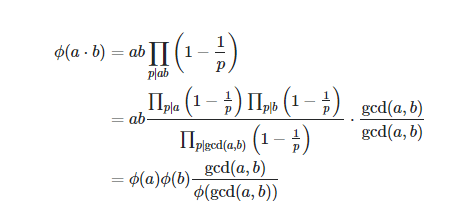
2018-hdu-7-E1

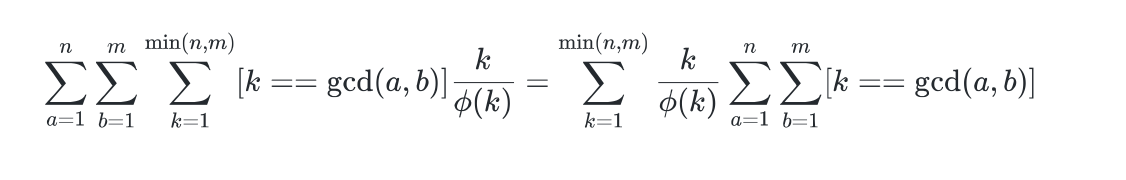
2018-hdu-7-E

所以就是枚举k，使得a，b的最大公因数是k，计算个数

所以右边的就是bzoj 1101

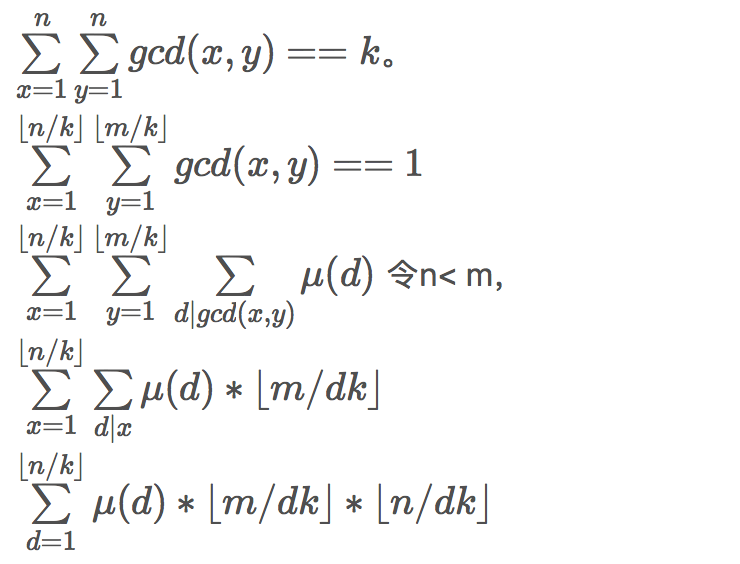
2018-hdu-7-E2

按取值分段分别处理，一个段内的和，可以用预处理出的莫比乌斯函数前缀和求出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
int n,m,tot,p;
ll mu[maxn],prime[maxn],sum[maxn],inv[maxn],phi[maxn];
bool notprime[maxn];
ll ans;
void Mobius(){
    tot=0;
    // memset(notprime,0,sizeof(notprime));
    mu[1]=1;notprime[1]=1;
    for(int i=2;i<=maxn-10;i++){
        if(!notprime[i]){
            prime[++tot]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=tot;j++){
            if(i*prime[j]>maxn-10) break;
            notprime[prime[j]*i]=1;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
    for(int i=1;i<=maxn-10;i++) sum[i]=sum[i-1]+mu[i];
}
void Euler(){
    for(int i=2; i<=maxn; ++i)
        phi[i]=0;
    phi[1]=1;
    for(int i=2; i<=maxn; ++i)
        if(!phi[i])
            for(int j=i; j<=maxn; j+=i){
                if(!phi[j])
                    phi[j]=j;
                phi[j]=phi[j]/i*(i-1);
            }
}
//分块计算
ll cal(int a,int b){
    if(a>b) swap(a, b);
    ll tmp=0;int pos;
    for(int i=1;i<=a;i=pos+1){
        pos=min(a/(a/i),b/(b/i));
        tmp+=1LL*(sum[pos]-sum[i-1])*(a/i)*(b/i);
    }
    return tmp;
}
void init(int len,int mod){
    inv[1]=1;
    for(int i=2;i<=len;i++)
        inv[i]=inv[mod%i]*(mod-mod/i)%mod;
}
int main(){
    Mobius();
    Euler();
    int T;scanf("%d",&T);
    while(T--){
        ans=0;
        scanf("%d%d%d",&m,&n,&p);
        int gcd_max=min(m,n);
        init(gcd_max, p);
        for(int k=1;k<=gcd_max;k++){
            ans+=cal(n/k, m/k)*k%p*inv[phi[k]]%p;ans%=p;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

H. Traffic Network inNumazu【不会

看题解的话，首先要知道LCA，这个东西

所以，先来补一波知识点吧！

LCA： least common acestors最近公共祖先；

我们可以考虑几种情况

通过染色来说明，这个我是看CSDN

每当一个结点由灰转黑的时候，就将它所在的集合合并到其父亲结点所在的集合中去。这样无论什么时候，任意一个黑色结点所在集合的代表元素就是这个结点向上的第一个灰色结点。

看完了图，应该可以理解离线算法（即这棵树是不会变的），假若一棵树存在动态更新，此时离线算法就显得有点力不从心了，但是在其他情况下，离线算法往往效率更高。

这里的Trajan算法的模拟过程可以看CSDN；

找了一道裸题，而且只有一个查询的水题练手：

POJ 1330
写了两段代码，但是思路都是一样的！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int maxn=1e4+10;
vector<int>edge[maxn];
vector<int>query[maxn];
int f[maxn],num[maxn],flag[maxn];
int ans,n;
bool vis[maxn];
void init(){
    memset(vis,0,sizeof(vis));
    memset(flag,0,sizeof(flag));
    for(int i=1;i<=n;i++){
        f[i]=i;
        edge[i].clear();
        query[i].clear();
    }
}
int find(int x){
    int y=x,tmp;
    while(f[x]!=x) x=f[x];
    while(f[y]!=x){
        tmp=f[y];
        f[y]=x;
        y=tmp;
    }
    return x;
}
void Tarjan(int x){
    int len=edge[x].size();
    int nex;
    for(int i=0;i<len;i++){
        nex=edge[x][i];
        Tarjan(nex);
        f[nex]=x;
    }
    vis[x]=true;
    len=query[x].size();
    for(int i=0;i<len;i++){
        nex=query[x][i];
        if(vis[nex]){
            ans=find(nex);
            return ;
        }
    }
}
int main(){
    int T;scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        init();
        int x,y;
        for(int i=1;i<n;i++){
            scanf("%d%d",&x,&y);
            flag[y]++;
            edge[x].push_back(y);
        }
        scanf("%d%d",&x,&y);
        query[x].push_back(y);
        query[y].push_back(x);
        for(int i=1;i<=n;i++){
            if(!flag[i])
                Tarjan(i);
        }
        printf("%d\n",ans);
    }
    return 0;
}

当然，网上的板子挺多的，调顺手的用！

但是，在这道题目中，我们的边的值会变，这很可能使我们的数的形状也在改变；所以我们需要看一下在线的方法！

唔……所以这道题目，今天估计都不会了！

在线的方法，我则看了ST算法！

然后，他又说是基于RMQ算法的，然后我又不会！天呐！我会啥呀，不知道之前都在干什么？发呆！

摘录一下，重点：【dp】

dp[i][j]表示从第i位开始，到第i + 2^j -1位的最大值或者最小值。

把它分成两部分，第一部分从i到i + 2 ^( j-1 ) - 1

第二部分从 i + 2 ^( j-1 ) 到 i + 2^j - 1

转移方程：

mm [ i ][ j ] = max ( mm [ i ][ j - 1 ] , mm [ i + ( 1 << ( j - 1 ) ) ][ j - 1 ] );

查询时，对于任意一个区间 l -- r，我们同样可以得到区间差值len = （r - l + 1）。

那么我们这一用小于2^k<=len的k 把区间分成可以交叉的两部分l到 l+2^（k）- 1, 到 r -(1<<k)+1到r的两部分。

然后我就开始做POJ 3264了

好啦！终于可以进入正题了，开始学习在线算法了！

2018-hdu-7-H-ST

ST算法是用来求解给定区间RMQ的最值；包含离线预处理(nlogn)和在线查询(o(1))；运用DP思想，求解区间最值；所以对于多组查询的时候，我们需要用ST算法。

I. Tree【未完成

dfs+分块

于是学了分块，bzoj 1086【无法验证正确与否的题目；

然而还是不会做！

TLE啦！！！！！！啊！！！！！！！！！！

【待补！！！！

J. Sequence

分块+矩阵快速幂

被二维矩阵思维禁锢了，应该开成三维的

1
2
3
4
5
6
7
8
9
10
Fn           D C 1      B
Fn-1    =    1 0 0  *   A
e            0 0 1      e
其中e是p/n的向下取整
也可以是
Fn           D C e      B
Fn-1    =    1 0 0  *   A
1            0 0 1      1

然后注意，在用矩阵运算时，每次都会申请一段新的空间，并且对其初始化，这样会导致时间剧增，因此，空间合适就好

同时，能用int就int，long long运算也会很慢的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
struct Mat{
    int row, col;
    int N[3][3];
    Mat(int row = 0 , int col = 0){
        memset(N, 0, sizeof(N));
        this -> row = row;
        this -> col = col;
    }
    Mat operator * (const Mat B) const {
        Mat A(row, B.col);
        for(int i = 0 ;i < row; i ++)
            for(int k = 0 ; k < col; k ++)
                for(int j = 0 ; j < B.col; j++){
                    A.N[i][j] = (A.N[i][j] + (ll)N[i][k] * B.N[k][j]%mod+mod)%mod ;
                }
        return A;
    }
    Mat operator ^ (int x) const {
        Mat A(row,row) , temp = *this;
        for(int i = 0 ; i < row; i ++)  A.N[i][i] = 1;
        while(x){
            if(x & 1)   A = A * temp;
            temp = temp * temp;
            x>>= 1;
        }
        return A;
    }
    
//    void Print(){
//        for(int i=0;i<row;i++){
//            for(int j=0;j<col;j++){
//                cout<<N[i][j]<<" ";
//            }
//            cout<<endl;
//        }
//    }
};
int main() {
    int T;scanf("%d",&T);
    int a,b,c,d,p,n;
    Mat B(3,3);Mat C(3,1);
    Mat BB(3,3);
    while(T--){
        B.N[0][2]=1;
        B.N[1][0]=1;B.N[1][1]=0;B.N[1][2]=0;
        B.N[2][0]=0;B.N[2][1]=0;B.N[2][2]=1;
        scanf("%d%d%d%d%d%d",&a,&b,&c,&d,&p,&n);
        if(n==1){
            printf("%d\n",a);
            continue;
        }else if(n==2){
            printf("%d\n",b);
            continue;
        }
        B.N[0][0]=d;B.N[0][1]=c;
//        B.Print();
        int now=3;int e=p/now;int r;
        int cnt=0;
        while(now<=n){
            cnt++;
            if(!e) r=n;
            else r=min(n,p/e);
//            cout<<now<<" "<<e<<" "<<" "<<r<<endl;
            C.N[0][0]=b;C.N[1][0]=a;C.N[2][0]=e;
//            C.Print();
            BB=B^(r-now+1);
//            B.Print();
            C=BB*C;
//            C.Print();
            b=C.N[0][0];a=C.N[1][0];
            now=r+1;e=p/now;
        }
        b=(b+mod)%mod;
        // cout<<cnt<<endl;
         printf("%d\n",b);
    }
    return 0;
}

K. Swordsman

IO好可怕！不知道有没有简单点的外挂！

然后，就是fread不可以自己直接式，要打开文件呐！

对于 k 种防御属性，分开进行从小到大排序，设立 k 个指针从最小处开始往最大处移动，对满足被杀死的条件的属性进行标记，当某只 monster 的所有防御属性都被标记时，更新剑士的魔法属性同时更新指针往后移动。时间复杂度 O(kn log n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cctype>
#include <cmath>
#include <vector>
using namespace std;
const int maxn=1e5+10;
namespace IO{
#define BUF_SIZE 100000
#define OUT_SIZE 100000
#define ll long long
    //fread->read
    bool IOerror=0;
    inline char nc(){
        static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE;
        if (p1==pend){
            p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin);
            if (pend==p1){IOerror=1;return -1;}
            //{printf("IO error!\n");system("pause");for (;;);exit(0);}
        }
        return *p1++;
    }
    inline bool blank(char ch){return ch==' '||ch=='\n'||ch=='\r'||ch=='\t';}
    inline void read(int &x){
        bool sign=0; char ch=nc(); x=0;
        for (;blank(ch);ch=nc());
        if (IOerror)return;
        if (ch=='-')sign=1,ch=nc();
        for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
        if (sign)x=-x;
    }
    inline void read(ll &x){
        bool sign=0; char ch=nc(); x=0;
        for (;blank(ch);ch=nc());
        if (IOerror)return;
        if (ch=='-')sign=1,ch=nc();
        for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
        if (sign)x=-x;
    }
    inline void read(double &x){
        bool sign=0; char ch=nc(); x=0;
        for (;blank(ch);ch=nc());
        if (IOerror)return;
        if (ch=='-')sign=1,ch=nc();
        for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
        if (ch=='.'){
            double tmp=1; ch=nc();
            for (;ch>='0'&&ch<='9';ch=nc())tmp/=10.0,x+=tmp*(ch-'0');
        }
        if (sign)x=-x;
    }
    inline void read(char *s){
        char ch=nc();
        for (;blank(ch);ch=nc());
        if (IOerror)return;
        for (;!blank(ch)&&!IOerror;ch=nc())*s++=ch;
        *s=0;
    }
    inline void read(char &c){
        for (c=nc();blank(c);c=nc());
        if (IOerror){c=-1;return;}
    }
    //fwrite->write
    struct Ostream_fwrite{
        char *buf,*p1,*pend;
        Ostream_fwrite(){buf=new char[BUF_SIZE];p1=buf;pend=buf+BUF_SIZE;}
        void out(char ch){
            if (p1==pend){
                fwrite(buf,1,BUF_SIZE,stdout);p1=buf;
            }
            *p1++=ch;
        }
        void print(int x){
            static char s[15],*s1;s1=s;
            if (!x)*s1++='0';if (x<0)out('-'),x=-x;
            while(x)*s1++=x%10+'0',x/=10;
            while(s1--!=s)out(*s1);
        }
        void println(int x){
            static char s[15],*s1;s1=s;
            if (!x)*s1++='0';if (x<0)out('-'),x=-x;
            while(x)*s1++=x%10+'0',x/=10;
            while(s1--!=s)out(*s1); out('\n');
        }
        void print(ll x){
            static char s[25],*s1;s1=s;
            if (!x)*s1++='0';if (x<0)out('-'),x=-x;
            while(x)*s1++=x%10+'0',x/=10;
            while(s1--!=s)out(*s1);
        }
        void println(ll x){
            static char s[25],*s1;s1=s;
            if (!x)*s1++='0';if (x<0)out('-'),x=-x;
            while(x)*s1++=x%10+'0',x/=10;
            while(s1--!=s)out(*s1); out('\n');
        }
        void print(double x,int y){
            static ll mul[]={1,10,100,1000,10000,100000,1000000,10000000,100000000,
                1000000000,10000000000LL,100000000000LL,1000000000000LL,10000000000000LL,
                100000000000000LL,1000000000000000LL,10000000000000000LL,100000000000000000LL};
            if (x<-1e-12)out('-'),x=-x;x*=mul[y];
            ll x1=(ll)floor(x); if (x-floor(x)>=0.5)++x1;
            ll x2=x1/mul[y],x3=x1-x2*mul[y]; print(x2);
            if (y>0){out('.'); for (size_t i=1;i<y&&x3*mul[i]<mul[y];out('0'),++i); print(x3);}
        }
        void println(double x,int y){print(x,y);out('\n');}
        void print(char *s){while (*s)out(*s++);}
        void println(char *s){while (*s)out(*s++);out('\n');}
        void flush(){if (p1!=buf){fwrite(buf,1,p1-buf,stdout);p1=buf;}}
        ~Ostream_fwrite(){flush();}
    }Ostream;
    inline void print(int x){Ostream.print(x);}
    inline void println(int x){Ostream.println(x);}
    inline void print(char x){Ostream.out(x);}
    inline void println(char x){Ostream.out(x);Ostream.out('\n');}
    inline void print(ll x){Ostream.print(x);}
    inline void println(ll x){Ostream.println(x);}
    inline void print(double x,int y){Ostream.print(x,y);}
    inline void println(double x,int y){Ostream.println(x,y);}
    inline void print(char *s){Ostream.print(s);}
    inline void println(char *s){Ostream.println(s);}
    inline void println(){Ostream.out('\n');}
    inline void flush(){Ostream.flush();}
#undef ll
#undef OUT_SIZE
#undef BUF_SIZE
};
struct Magic{
    int val,id;
    bool operator<(const Magic& other)const{
        return val<other.val;
    }
}Monster[6][maxn];
int man[6];
int cnt[6];//表示这个技能，在Monster[i][cnt[i]].val>man[i]
int vis[maxn];//表示这个怪兽已经满足几个技能了
int b[maxn][6];
int main(){
    int T;IO::read(T);
    int n,k;
    while(T--){
        IO::read(n); IO::read(k);
        for(int i=0;i<k;i++) IO::read(man[i]);
        for(int i=0;i<n;i++){
            for(int j=0;j<k;j++){
                IO::read(Monster[j][i].val);
                Monster[j][i].id=i;
            }
            for(int j=0;j<k;j++){
                IO::read(b[i][j]);
            }
        }
        
        for(int i=0;i<k;i++){
            sort(Monster[i], Monster[i]+n);
        }
        
        bool flag;
        int id;
        int ans=0;
        memset(vis,0,sizeof(vis));
        memset(cnt,0,sizeof(cnt));
        while(true){
            flag=false;//表示是否加入了新的怪兽
            for(int i=0;i<k;i++){
                while(cnt[i]<n&&Monster[i][cnt[i]].val<=man[i]){
                    id=Monster[i][cnt[i]].id;
                    vis[id]++;
                    if(vis[id]==k){//可以杀死怪兽，并且提升技能了
                        for(int j=0;j<k;j++){
                            man[j]+=b[id][j];
                        }
                        flag=true;
                        ans++;
                    }
                    cnt[i]++;
                }
            }
            if(!flag) break;
        }
        IO::println(ans);
        for(int i=0;i<k-1;i++){
            IO::print(man[i]);IO::print(' ');
        }
        IO::println(man[k-1]);
    }
    return 0;
}

碎碎念

2018.08.14 午

嗝！吃多了！

然后发现自己变懒了！脚上不知道长了什么东西，红了！

难道是我我要长高了吗？姑且这么安慰自己了！

转载请注明出处，谢谢。

愿 我是你的小太阳


买糖果去喽