2018 Multi-University Training hdu Contest 6

Posted on | In , | Visitors:

嚯嚯嚯！补题！

hdu多校总链接

补题： 6题/12题

  • 欧拉降幂
  • 费马小定理
  • GCD
  • LCM
  • 快速幂
  • 区间DP
  • 搜索
  • 并查集
  • lucas
  • Tarjan
  • 缩点
  • nth_element(begin(), begin() + needs, end());

A. oval-and-rectangle

这题英文不好，跑偏了！

  • 这里的side居然不是边的意思，导致我们认为纵坐标是c/2，怎么能默认y就是坐标y呢！
  • 这里的c不可以是横坐标的选择，我们还以为一条边是c，那么也可以是x是c/2

所以总结来说，英文不好！

最后，其实跳出来的时候，踩进的坑则是，输出格式。题目要求的是丢弃末尾，而不是四舍五入。但我不知道的是用%.6lf输出的是经过四舍五入的。所以需要先化成整数，再用floor函数之后，在转换为小数！

所以，WA的几发都是这个原因。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double PI = acos(-1.0);
int main() {
    int T;
    scanf("%d",&T);
    while(T--){
        double a,b;
        scanf("%lf%lf",&a,&b);
//        double angle2 = PI/2;
//        double angle1 = asin(b/a);
//        double tmp3 = a*sin(2*angle2)+2*a*angle2-b*(cos(2*angle2)-1);
//        double tmp2 = a*sin(2*angle1)+2*a*angle1-a*a/b*(cos(2*angle1)-1);
        long long ans = floor((a * PI + 2 * b) * 1000000);
        printf("%.6lf\n", (double)ans / 1000000);
//        printf("%.6lf\n",tmp2);
//        printf("%.6lf\n",0.5*(tmp2+tmp3));
    }
    return 0;
}

B. Bookshelf

先放点数论的知识点：

欧拉降幂公式：a^x ≡a^(x modϕ(p)+ϕ(p)) (mod p)

费马小定理： $\frac a b\%mod=a*b^{mod-2}\%mod$

最大公约数(gcd)的性质：

交换律 gcd(a,b)=gcd(b,a)

分配律 gcd(ma,mb)=m * gcd(a,b)

​ gcd(a, lcm(b, c)) = lcm(gcd(a, b),gcd(a, c))

​ lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))

【最大公因子lcm】

$gcd(a^{F_x}+c,a^{F_y}+c) = 2^{gcd(F_x,F_y)}+c = 2^{F_{gcd(x,y)}}+c$

image-20180811152621033

在写代码的时候，如果将$2^{F_g}$的值作为新的$f[i]$先预处理，但这时会TLE，所以我们需要继续观察

$f[i]=2^{F[i]}=2^{F[i-1]+F[i-2]}=2^{F[i-1]}2^{F[i-2]}=f[i-1]f[i-2]$

这样就不用每次调用函数了

我居然把快速幂写错了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
const int maxn=2e6+10;
ll f[maxn],fac[maxn],inv[maxn],a[maxn];
int n,k;
ll kpow(ll a,ll b){
    ll ans=1,base=a;
    while(b){
        if(b&1) ans=(ans*base)%mod;
        base=base*base%mod;
        b>>=1;
    }
    return ans;
}
void init(){
    f[0]=1;f[1]=2;
    fac[0]=fac[1]=1;
    inv[1]=1;
    for(int i=2;i<maxn;i++){
        f[i]=(f[i-2]*f[i-1])%mod;
        fac[i]=1LL*fac[i-1]*i%mod;
        inv[i]=kpow(fac[i], mod-2);
    }
}
ll Cnm(ll n,ll m){
    if(n<m) return 0LL;
    if(n==m||m==0) return 1LL;
    if(m==1||m==n-1) return n;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main(){
    init();
    int T;scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&k);
        ll ans=0;
        memset(a, 0, sizeof(a));
        for(int g=n;g>=1;g--){
            if(n%g==0){
                ll j=n/g;
                a[g]=Cnm(j+k-1, j);
                for(int i=2*g;i<=n;i+=g){
                    a[g]=(a[g]-a[i]+mod)%mod;
                }
//                cout<<g<<" "<<f[g]<<" "<<kpow(2,f[g])<<endl;
//                ans=(ans+a[g]*(kpow(2,f[g])-1+mod)%mod)%mod;
                ans=(ans+a[g]*(f[g]-1+mod)%mod)%mod;
            }
        }
        ll sum=Cnm(n+k-1, n);
        ans=ans*kpow(sum, mod-2)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

C. Ringland

D. Shoot Game

区间DP题目，刚开始想了很久的DP设计，然后

果断看了题解（发现了一句话

只需要考虑像所有障碍物的两个端点去发射射线，就能包含所有的情况

可以想象一下，就明白了（这句话很重要哦！

然后所需的就是按角序对2n个点重新排序，（注意按一般来说，我们写的是k，但是角序，是按照顺时针来的，不是按照k的值的大小来的；同时分式变的时候，乘以的分母不一定是整数，所以，导致了我一开始的<重载是反着的

之后，我们需要将原来序号和新序号对应起来

之后，找到最大障碍物，（这里当时思考了一个问题，如果有两个最大值怎么办，画一个图就可以知道了

之后，就根据dp等式进行了转移

这里如果有两个斜率的话，会增加复杂度，应该不会导致错误的发生，但从我们的思路来说，是通过顺序枚举斜率来考虑的，所以，发现了一个新的函数unique，同时，我终于会在结构体里重载运算符了，（因为在结构体里写有好多const值，我总是忘记写第二个const）

之又发生了一个问题，就是如果删去重复元素的话，会导致有些元素找不到对应的新坐标

所以WA了

附上AC代码：【因为刚开始的问题，所以实际上我们可以将oldNo和left这两个变量删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=610;
struct Point{
    ll x,y;
    int oldNo;
    bool left;
    
    Point() {}
    Point(ll _x,ll _y,int _o,bool _l):x(_x),y(_y),oldNo(_o),left(_l) {}
    bool operator <(const Point& other)const{
        return y*other.x>=x*other.y;
    }
    
    bool operator ==(const Point& other)const{
        return y*other.x-x*other.y==0;
    }
    
}point[maxn];
int h[maxn],l[maxn],r[maxn],w[maxn];
ll dp[maxn][maxn];
int main(){
    int T;scanf("%d",&T);
    while(T--){
        int n;scanf("%d",&n);
        int m=1;
        for(int i=1;i<=n;i++){
            scanf("%d%d%d%d",&h[i],&l[i],&r[i],&w[i]);
            point[m].x=l[i]; point[m].y=h[i];
            point[m+1].x=r[i];point[m+1].y=h[i];
            point[m].oldNo=point[m+1].oldNo=i;
            point[m].left=true;point[m+1].left=false;
            m+=2;
        }
        m--;
        sort(point+1, point+m+1);
        m=unique(point+1, point+m+1)-(point+1);
        
        //这里如果这样写的话，会有一些斜率相同的点被改变的
//        for(int i=1;i<=m;i++){
////            cout<<point[i].x<<" "<<point[i].y<<endl;
//            if(point[i].left){
//                l[point[i].oldNo]=i;
//            }else{
//                r[point[i].oldNo]=i;
//            }
//        }
        for(int i=1;i<=n;++i) {
            l[i]=lower_bound(point+1,point+1+m,Point(l[i],h[i],i,true))-point-1;
            r[i]=lower_bound(point+1,point+1+m,Point(r[i],h[i],i,false))-point-1;
        }
        
//        for(int i=1;i<=n;i++){
//            cout<<l[i]<<" "<<r[i]<<endl;
//        }
        for(int len=1;len<=m;len++){
            for(int i=1;i+len-1<=m;i++){
                int j=len+i-1;
                
                //寻找最大值的点
                int left=-1,right=-1,val=-1;
                for(int k=1;k<=n;k++){
                    if(i<=l[k]&&r[k]<=j&&w[k]>val){
                        left=l[k];right=r[k];
                        val=w[k];
                    }
                }
                
                //如果没有点在其中，则这一段不需要消耗灵力
                if(val==-1){
                    dp[i][j]=0;
                    continue;
                }
                
                dp[i][j]=(1LL<<60);
                for(int k=left;k<=right;k++){
                    dp[i][j]=min(dp[i][j],dp[i][k-1]+dp[k+1][j]+val);
                }
            }
        }
        printf("%lld\n",dp[1][m]);
    }
    return 0;
}

I. Werewolf

不存在铁定是村民的情况；环中只有一条狼标记的边，则指向的点定是狼，之后通过指向狼的边标记是村民的点定是狼

可惜，不会写代码！

题解中说的是，先不考虑狼人边，如果得到的是基环树（基环树就是树加上了一条边，使之成为环），则这里都可以是村民；

如果得到的是树，进行分类讨论。

我们需要的是铁狼的数量！

然后网上有

  • 搜索+并查集（并查集就是把指认是村民的边缩点，即把那个特殊判断的环缩在一起，如果属于同一集合，说明是一个环内！嗯嗯，终于懂了！感觉并查集太厉害了！（好吧，今天发现自己原来反应真的很迟钝，外加很蠢！估计是被某人说蠢的吧！

    【不过，为了凸显自己的特别，所以不可以夸我，只可以黑我……emmmm 这理由，我想咬人！哼！

    哦，对，这里写的时候，只输出了ans，找bug一万年，然后发现bug，呼，又是一万年的命啊……

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    #include <iostream>
    #include <cstdio>
    #include <algorithm>
    #include <cstring>
    #include <queue>
    using namespace std;
    const int maxn=1e5+10;
    int num,n,ans;
    int head[maxn],f[maxn];
    bool vis[maxn];
    int Find(int x){
        if(f[x]==x) return x;
        else return f[x]=Find(f[x]);
    }
    void Union(int x,int y){
        int fx=Find(x);int fy=Find(y);
        if(fx==fy) return ;
        else f[fy]=fx;
    }
    struct Edge{
        int u,v,next,w;
    }edge[maxn<<1];
    void addEdge(int u,int v,int w){//向前插入的链表
        edge[num].u=u;
        edge[num].v=v;
        edge[num].w=w;
        edge[num].next=head[u];
        head[u]=num++;
    }
    void init(){
        memset(head, -1, sizeof(head));
        memset(vis, 0, sizeof(vis));
        scanf("%d",&n);
        for(int i=1;i<=n;i++) f[i]=i;
        num=0;ans=0;
        int x;char s[20];
        for(int i=1;i<=n;i++){
            scanf("%d%s",&x,s);
            if(s[0]=='w')
                addEdge(x, i, 1);
            else{
                addEdge(x, i, 0);
                Union(i,x);//将指认村民的缩点，形成的环，进行缩点
            }
        }
    }
    int main(){
        int T;scanf("%d",&T);
        while(T--){
            init();
            queue<int>q;
            for(int i=0;i<=num;i++){
                int u = edge[i].u,v=edge[i].v,w=edge[i].w;
                if(Find(u)==Find(v)&&w==1&&vis[v]==0){//特殊判断
                    ans++;
                    q.push(u);
                    vis[u]=1;
                }
            }
            while(!q.empty()){
                int u = q.front();
                q.pop();
                for(int i=head[u];i!=-1;i=edge[i].next){
                    int v=edge[i].v,w=edge[i].w;
                    if(w) continue;
                    if(vis[v]) continue;
                    ans++;
                    q.push(v);
                }
            }
            printf("0 %d\n",ans);
        }
        return 0;
    }

  • 缩点（tarjan）【这个比较适合我啦！但写起来比较麻烦，然后我就写爆了！额……给个框架，带我再学习一遍，重来吧！太惨了……过了，太惨了……( ･᷄ὢ･᷅ )

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    #include <cstdio>
    #include <cstring>
    #include <cmath>
    #include <algorithm>
    #include <iostream>
    const int maxn=1e5+10;
    using namespace std;
    struct edge{
        int next,to,w;
    }ed[maxn<<1],e[maxn<<1];
    void add(int u,int v,int w){
        ed[cnt].w=w;
        ed[cnt].to=v;
        ed[cnt].next=head[u];
        head[u]=cnt++;
    }
    void add2(int u,int v,int w){//反向建边
        e[tot].w=w;
        e[tot].to=v;
        e[tot].next=first[u];
        first[u]=tot++;
    }
    void tarjan(int root){
        
    }
    void dfs(int i){//i是铁狼
        for(int j=first[i];~j;j=e[j].next){
            int v=e[j].to;
            if(e[j].w==1){
                ans++;
                dfs(v);
            }
        }
    }
    int main(){
        int T;
        scanf("%d",&T);
        while(T--){
            int n;
            scanf("%d",&n);
            cnt=
            for(int i=1;i<=n;i++){
                int x;char s[50];
                scanf("%d%s",&x,s);
                if(s[0]=='w'){//0为狼边，1为村民边
                    add(i, x, 0);
                    add2(x, i, 0);//反向建图
                }else{
                    add2(x, i, 1);
                    add(i, x, 1);
                }
            }
            for(int i=1;i<=n;i++){
                if(!dfn[i]) tarjan(i);
            }
            
            //……一些丑陋的代码
            
            printf("0 %d\n",ans);
        }
    }

  • 基环树（题解！没兴趣- - 不过代码看懂了

  • 反向建边（这个还是不错的呢

K. Sacul

主要是数学的分析能力，这点需要我们掌握一些定理，同时进行等式的推导；感觉搞这个以后也是有用的呢！听到一点，就积累一点好啦！

首当其冲的就是这个题目的名称，出题人取名字还是很友好的啦！虽然总是在黑人！

其实本质上就是把n,m按进制p拆位一一组合数后乘起来。

其他知识点很小，暂且不解释了！

刚开始写完，爆空间了，于是就不先预处理inv数组了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
//题目要求的最大质数
//1299709+1e5+1
const int maxn=1400000;
const int maxx=1e5;
const int mod=1e9+7;
ll fac[maxn+10];
//ll inv[maxn+10];
ll p[maxn+100],prime[maxn/5];
ll tot,c,n,k,ans,a;
ll kpow(ll a,ll b){
    ll ans=1,base=a;
    while(b){
        if(b&1) ans=ans*base%mod;
        base=base*base%mod;
        b>>=1;
    }
    return ans;
}
//扩展欧几里得
ll extgcd(ll a,ll b,ll &x,ll &y){
    ll d=a;
    if(b!=0){
        d=extgcd(b,a%b,y,x);
        y-=(a/b)*x;
    }
    else{
        x=1;y=0;
    }
    return d;
}
//求逆元
ll inv(ll a){
    ll x,y,d=extgcd(a,mod,x,y);
    x=(x%mod+mod)%mod;
    return x;
}
void init(){
    fac[0]=fac[1]=1;
//    inv[0]=inv[1]=1;
    for(int i=2;i<=maxn;i++){
        fac[i]=fac[i-1]*i%mod;
//        inv[i]=kpow(fac[i], mod-2)%mod;
//        inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod;
    }
    //求质数，这个我好像很少用呢！不过这个是不是叫质数筛啊！zsp上课讲过呢！但是我忘记了哪节课了！
    p[1]=1;tot=0;
    for(int i=2;i<=maxn;i++){
        if(!p[i]){
            p[i]=i;
            prime[++tot]=i;
        }
        for(int j=1;j<=tot&&prime[j]*i<=maxn;j++){
            p[i*prime[j]]=prime[j];
            if(p[i]==prime[j]) break;
        }
    }
//    cout<<prime[tot]<<endl;
}
int main(){
    init();
    
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld%lld",&c,&n,&k);
        ans=0;
        for(int j=1;j<=k;j++){
            a=fac[j+prime[c]]*inv(fac[prime[c]-1])%mod*inv(fac[j+1])%mod;
            if(a<0) a+=mod;
            if(a==1) ans=(ans+n)%mod;
            else if(a>0){
                //刚开始这里是连在一起写的，发现分开写可以减少空间，但明明是多了变量呢！可能和内部有关吧！
                ll e =(kpow(a, n)-1);
                ll d=kpow(a-1, mod-2);
                e=e*d%mod;e=e*a%mod;
                ans=(ans+e)%mod;
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}

L. Pinball

物理忘光了，然后作业帮是害人的！

  • 模拟不会，因为不懂原理。所以理科不好的人，不该来到理工学院的！

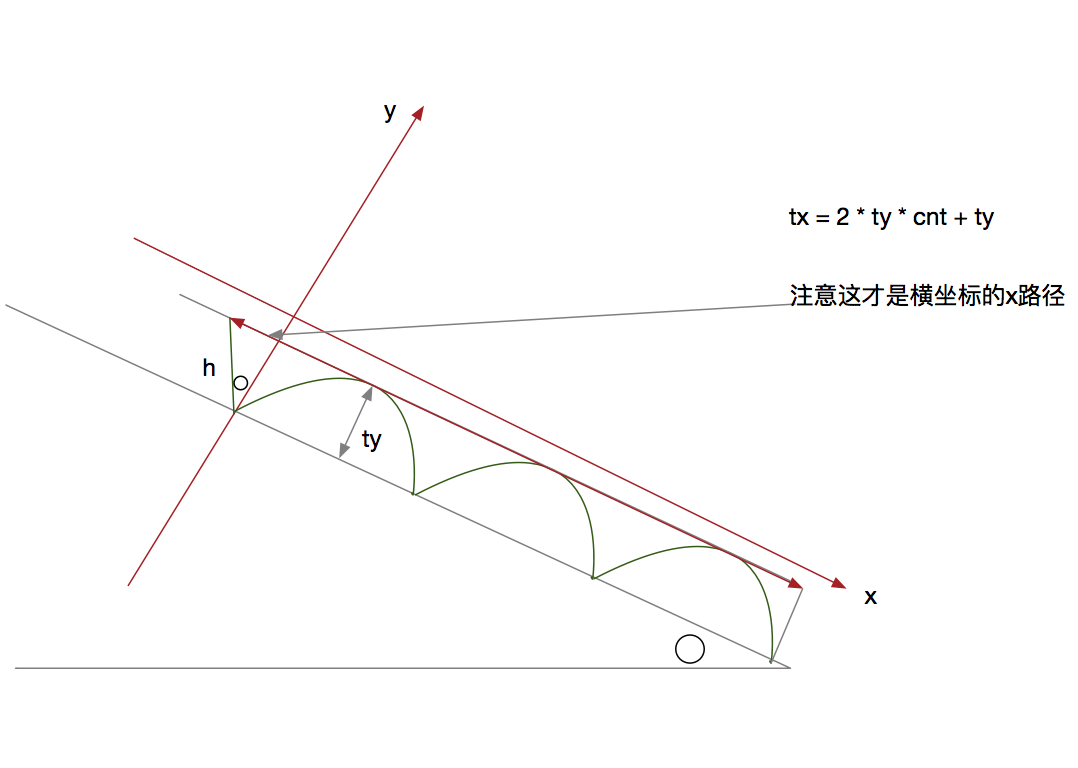
  • 不用一般坐标系，而是使用沿着斜面和垂直斜面（博博的思路很棒呢！只是没戴眼镜的我迷迷糊糊啊～什么都没听见

    然后呢，x方向就是匀加速运动，y方向就是周期运动，画个图理解一下吧！

    然后呢，这里有一个细节，感觉也是我物理会犯的错误，就是少了一条线段

2018-hdu-6-L

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const double g = 9.8;
const double PI = acos(-1.0);
const double EPS = 1e-6;
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        double a, b, x, y;
        scanf("%lf%lf%lf%lf", &a, &b, &x, &y);
        a *= -1;
        double angle = atan(b / -a);
        double ax = g * sin(angle), ay = g * cos(angle);
        double dy = y - b * x / a;
        double l = (-x)/cos(angle)+dy*sin(angle);
        double t = sqrt(2*l/ax);
        double h = dy * cos(angle);
        
        double ty = sqrt(2*h/ay);
        
        int ans=(t-ty)/(2*ty)+1;
        printf("%d\n", ans);
    }
}

碎碎念

2018.08.13 晚

感觉STL中的一些库函数真的是很神奇呢！

这次CF上的一题，发现了一个新的函数，

1
nth_element(begin(), begin() + needs, end());

返回，begin到end之间，前needs个按顺序排序，可以减少时间复杂度

转载请注明出处，谢谢。

愿 我是你的小太阳


买糖果去喽