信号与系统-笔记

信号与系统 概念与公式整理

信号与系统——概念篇

1. 线性系统

• 可分解性
• 零状态线性
• 零输入线性

注 完全响应不一定是线性的哦！！！

2. 零输入响应 与 零状态响应

• 当给出$ y^{(j)}(0_-) $ ，则先计算零输入响应：

            $ y_{zi}^{(j)}(0_+)=y_{zi}^{(j)}(0_-)=y^{(j)}(0_-) $        
  

计算零输入的时候，激励$f(t)=0$，所以此时求的是齐次方程，只有齐次解$y_h(t)$

• 当给出$ y^{(j)}(0_+) $ ，则先计算零状态响应：

            $y_{zs}^{(j)}(0_-)=0    =>    y_{zs}^{(j)}(0_+)$，**根据系数匹配法，即观察$\delta^{(j)}$的系数**
  

计算零状态响应的时候，这个时候的解为$y(t)=y_h(t)+y_p(t)$，此时可以讨论t>0的情况，因为零状态响应么！

然后设定齐次解和特定解的形式，和求解微分方程是一样的。

然后先将特解带入方程，求的系数；

再将两者加和所得到的全响应方程，带入初始值（初始值是指$0_+$，初始状态是指$0_-$），求解得系数的值。

一般来说，这里的$f(t)=\epsilon(t)$，所以可以设特解为$P$。

注 这里的解需要加上$t>=0$或$k>=0$

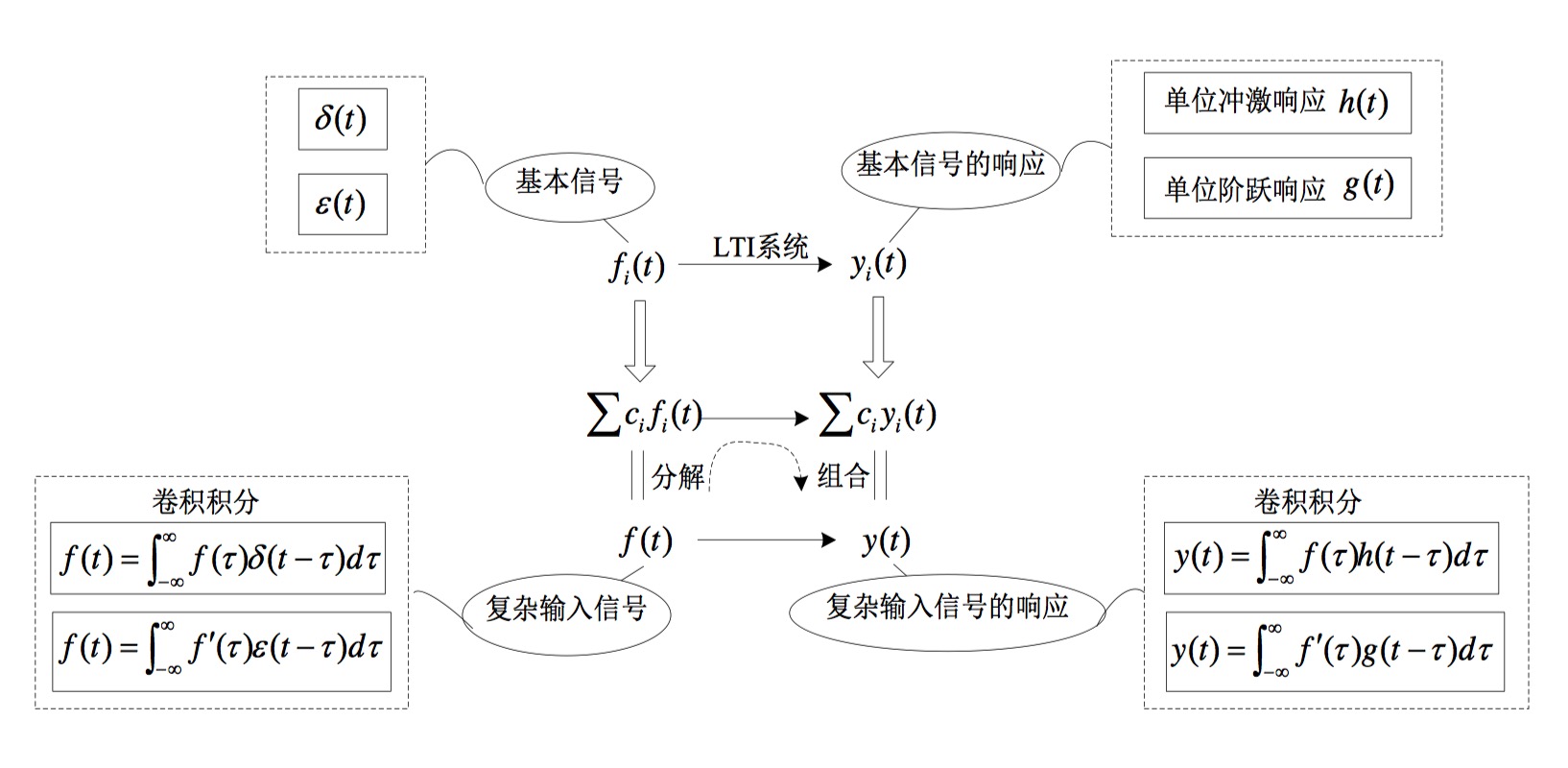
3. 冲激（序列）响应 与 阶跃响应

建议先算阶跃响应（有特解哦），然后冲激响应则可以通过$h(\iota)=\frac{dg(t)}{dt}$或$h(k)=g(k)-g(k-1)$

否则需算$ g(t)=\int_{-\infty}^th(\iota)d\iota$或$g(k)=\displaystyle\sum_{i=-\infty}^{k}h(i)$来求得

否则，一般来说由于阶跃响应有特解，结果里会有常数项，需要凑一下。

且求冲激响应的时候，同求零状态响应的方法相同。

注 不要忘记表达式之后一般会加上$\epsilon(t)$或$\epsilon(k)$，因为是零状态响应。

4. 卷积 与 卷积和

意义：

零状态响应等于输入信号与单位冲激（序列）响应的卷积。

$y_{zs}(t)=f(t)*h(t)$

$y_{zs}(k)=f(k)*h(k)$

图解法

求某一时刻的卷积值比较方便。

换元->反转平移->乘积->积分/求和

公式法

$y_{zs}(t)=f(t)*h(t)=\int_{-\infty}^{\infty}f(\iota)h(t-\iota)d\iota$

其中卷积的时候$f(\iota)$中间的变量不是$t$，且在$f_1(t)和f_2(t)$都含有$\epsilon(t)$，并且确定积分上下限之后，等式之后需加上$\epsilon(t)$

$y_{zs}(k)=f(k)*h(k)=\displaystyle\sum_{i=-\infty}^{\infty}f(i)h(k-i)$

卷积和加上的是$\epsilon(k)$，同时注意运用等比求和公式的时候，如果公比为1的时候，要特殊处理的

性质

见公式篇

复合系统

• 并联：$h(t)=h_1(t)+h_2(t)$
• 级联：$h(t)=h_1(t)*h_2(t)$

卷积和的不进位乘法

f(k)=所有两序列序号之和为k 的那些样本乘积之和

5. 模拟框图

延迟器：连续 T

延迟单元：离散 D

6. 离散 与 连续

	连续	离散
自变量	t	k
正弦函数角速度	$\omega$	$\Omega$
卷积	$\int$	$\sum$

7. 时域分析 与 频域分析

8. 信号的正交

正交

对于复数而言：$\int_{t_1}^{t_2}\phi_1(t)\phi_2^*(t)dt=0$

对于实数而言：$\int_{t_1}^{t_2}\phi_1(t)\phi_2(t)dt=0$

意义：$\phi_1(t)$和$\phi_2(t)$ 在区间$(t_1,t_2)$内正交。

正交函数集

$\int_{t_1}^{t_2}\phi_i(t)\phi_j^*(t)dt=\{^{0,\ \ \ \ \ \ \ \ \ \ i\not=j}_{K_i\not=0,\ \ \ \ i\not=j}$

若$K_i=1$，则为标准正交函数集

若在正交函数集${\phi_1(t),\phi_2(t),\dots,\phi_n(t)}$外，不存在$\int_{t_1}^{t_2}\phi(t)\phi_i^(t)dt=0\ \ \ \ \ (i=1,2,\cdots,n)$，则称此函数集为*完备函数集。

正交函数集的误差矢量为零。

信号的正交分解

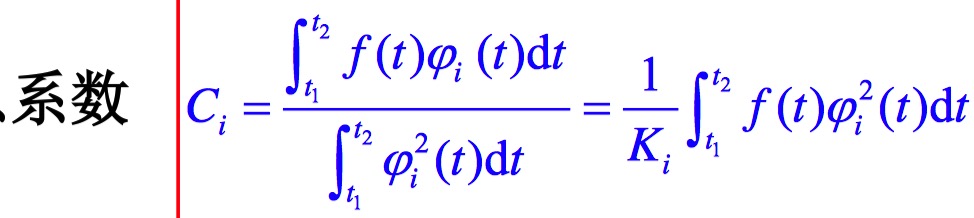
可知：完备正交函数集的均方误差为零。

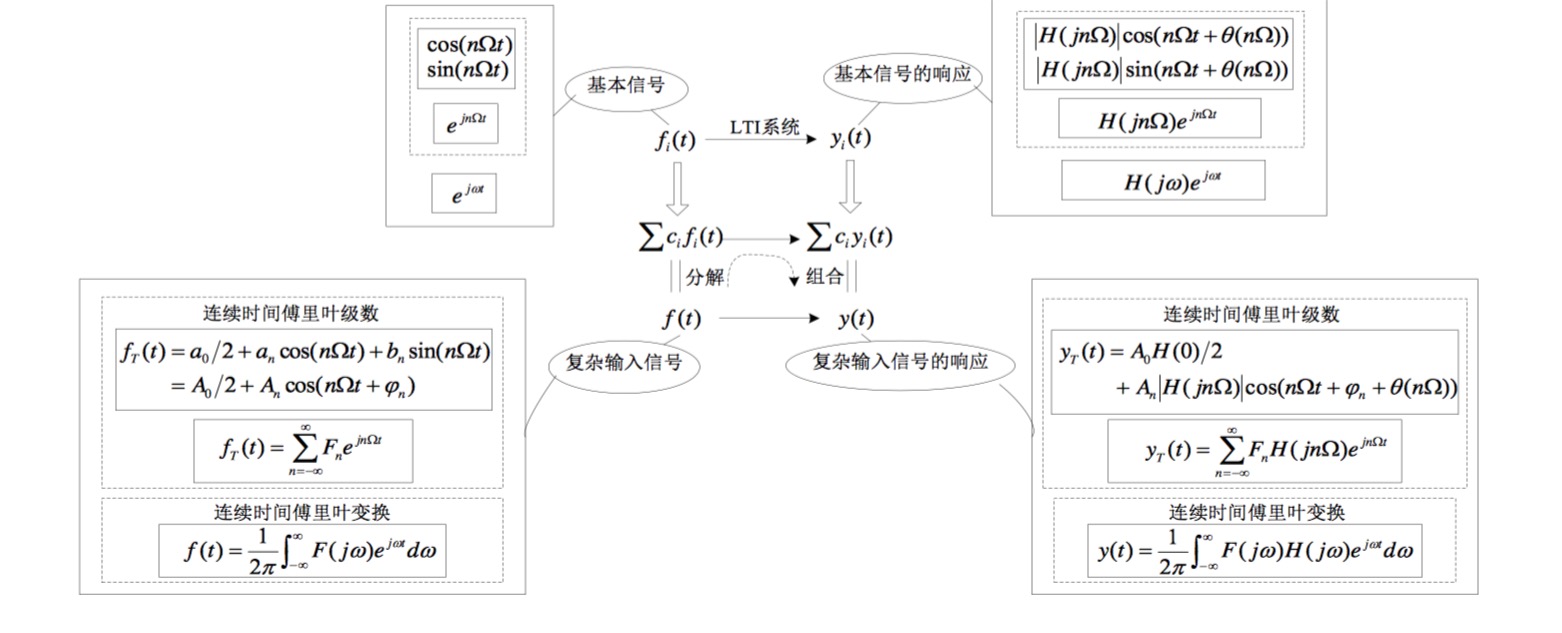
9. 傅立叶级数

分类

• 三角形式

  $f(t)=\frac{a_0}2+\displaystyle\sum_{n=1}^{\infty}a_ncos(n\Omega t)+\sum_{n=1}^{\infty}b_nsin(n\Omega t)=\frac {A_0} 2+\sum_{n=1}^{\infty}A_ncos(n\Omega t+\phi_n)$

  $A_n=\sqrt{a_n^2+b_n^2}$ $\phi(n)=-arctan \frac {b_n}{a_n}$

  $a_n=A_ncos\phi_n$ $b_n=-A_nsin\phi_n$

• 虚指数形式

$f(t)=\frac12\displaystyle\sum_{n=-\infty}^{\infty}A_ne^{j\phi_n}e^{jn\Omega t}=\sum_{n=-\infty}^{\infty}F_ne^{jn\Omega t}$

$F_n=\frac12A_ne^{j\phi_n}=|F_n|e^{j\phi_n}=\frac12(a_n-jb_n)$ $|F_n|=\frac12A_n $

注：

1. $f(t)=\frac {A_0} 2+\sum_{n=1}^{\infty}A_ncos(n\Omega t+\phi_n)$为标准形式
2. 这里的$\Omega=\frac{2\pi}T$

傅立叶系数

$a_n=\frac 2 T\int_{-\frac T 2}^{\frac T 2}f(t)cos(n\Omega t)dt$

$b_n=\frac 2 T\int_{-\frac T 2}^{\frac T 2}f(t)sin(n\Omega t)dt$

$F_n=\frac1T\int_{-\frac T2}^{\frac T 2}f(t)e^{-jn\Omega t}dt$

分量

• 直流分量

  $\frac{a_0}2=\frac 1 T\int_{-\frac T 2}^{\frac T 2}f(t)dt$

  $F_0=\frac 1 T\int_{-\frac T 2}^{\frac T 2}f(t)dt$

• 余弦分量

  $a_n=\frac 2 T \int_{-\frac T 2}^{\frac T 2}f(t)cos(n\Omega t)dt$

• 正弦分量

  $b_n=\frac 2 T \int_{-\frac T 2}^{\frac T 2}f(t)sin(n\Omega t)dt$

图像

若上下不对称，则含有直流分量

若偶函数 含有余弦波 没有正弦波

若奇函数 含有正弦波 没有余弦波

奇谐：$f(t)=-f(t\pm\frac T 2)$ 波形沿时间轴（横轴）平移半个周期后与原波形相对于时间轴像对称

偶谐：$f(t)=f(t\pm \frac T 2)$ 波形沿时间轴平移半个周期后与原波形完全重叠

奇谐，偶谐看二分之一 （奇谐上图，偶谐下图）

滤波，滤掉部分，高低频，上下部分……

傅立叶变换

$F(j\omega)=\displaystyle\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$ $F( j\omega)$称为$f(t)$的傅里叶变换

$f(t)=\frac 1{2\pi}\int_{-\infty}^{\infty}F(j\omega)e^{j\omega t}d\omega$ f(t)称为$F( j\omega)的$傅立叶逆变换

常用函数的傅立叶变换

1. 单边指数函数

$F(j\omega)=\frac 1{a+j\omega}$

$e^{-\alpha t}\epsilon(t)\leftrightarrow \frac 1{a+j\omega}$

$|F(j\omega)|=\frac 1{\sqrt{a^2+\omega^2}}$

$\phi(\omega)=-arctan\frac{\omega}{\alpha}$

1. 双边指数函数

$e^{-\alpha|t|}\leftrightarrow\frac{2\alpha}{\alpha^2+\omega^2}$

1. 门函数

$g_\iota(t)\leftrightarrow \iota Sa(\frac {\omega\iota}{2})$ [周期门函数$F_n=\frac \iota TSa(\frac{n\Omega\iota}2)$]

1. 冲激函数

   $\delta(t)\leftrightarrow1$

   $\delta’(t)\leftrightarrow j\omega$

   $\delta^{n}(t)\leftrightarrow (j\omega)^n$

2. 阶跃函数

   $\because \epsilon(t)=\frac12+\frac12sgn(t)$

   $\therefore \epsilon(t)=\pi\delta(\omega)+\frac1{j\omega}$

3. $1\leftrightarrow 2\pi\delta(\omega)$

4. 符号函数

$sgn(t)\leftrightarrow \frac 2 {j\omega}$

傅立叶变换的性质

线性性质

若 $f_1(t)\leftrightarrow F_1(j\omega)$ $f_2(t)\leftrightarrow F_2(j\omega)$

则 $af_1(t)+bf_2(t)\leftrightarrow aF_1(j\omega)+bF_2(j\omega)$

奇偶性

若 $f(t)\leftrightarrow F(j\omega)$

则 $f(-t)\leftrightarrow F(-j\omega)$

$F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$

• 若$f(t)$为实函数的时候

  $F(j\omega)=\int_{-\infty}^{\infty}f(t)cos(\omega t)dt-j\int_{-\infty}^{\infty}f(t)sin(\omega t)dt$

  $R(\omega)=\int_{-\infty}^{\infty}f(t)cos(\omega t)dt$

  $X(\omega)=-\int_{-\infty}^{\infty}f(t)sin(\omega t)dt$

  $R(\omega)= R(–\omega)$

  $X(\omega) = – X (–\omega)$

  $|F(j\omega)| = |F(– j\omega)|$

  $\phi(ω) = – \phi(–ω)$

  $f(-t)\leftrightarrow F(-j\omega)=F^*(j\omega)$

  • 若$f(t)$为实偶函数的时候

    $X(\omega) =0$

    $ F(j\omega)=2\int_{-\infty}^{0}f(t)cos(\omega t)dt$

    若$f(t)$为实奇函数的时候

    $R(\omega)=0$

    $ F(j\omega)=-2j\int_{-\infty}^{0}f(t)sin(\omega t)dt$

• $f(t)=jg(t)$为虚函数的时候

  $F(j\omega)=j\int_{-\infty}^{\infty}g(t)cos(\omega t)dt+\int_{-\infty}^{\infty}g(t)sin(\omega t)dt$

  $R(\omega)=\int_{-\infty}^{\infty}g(t)sin(\omega t)dt$

  $X(\omega)=\int_{-\infty}^{\infty}g(t)cos(\omega t)dt$

  $R(\omega)= -R(–\omega)$

  $X(\omega) = X (–\omega)$

  $|F(j\omega)| = |F(– j\omega)|$

  $\phi(ω) = – \phi(–ω)$

  $f(-t)\leftrightarrow F(-j\omega)=-F^*(j\omega)$

对称性

若 $f(t)\leftrightarrow F(j\omega)$

则 $F(jt)\leftrightarrow2\pi f(-\omega)$

尺度变换特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $f(at)\leftrightarrow \frac 1 {|a|}F(j \frac \omega a)$

1. 0<a<1 时域扩展，频带压缩。
2. a>1 时域压缩，频带扩展。信号的持续时间与信号占有频带成反比

信号的持续时间与信号占有频带成反比

时移特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $f(t\pm t_0)\leftrightarrow e^{\pm j\omega t_0}F(j\omega)$

$f(at-b)\leftrightarrow \frac 1 {|a|}e^{-j\omega \frac b a}F(j\frac \omega a)$

频移特性

若 $f(t)\leftrightarrow F(j\omega)​$

则 $e^{\mp j\omega_0 t}f(t) \leftrightarrow F[j(\omega\pm \omega_0)]$

时域微分特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $f^{(n)}(t)\leftrightarrow (jw)^nF(j\omega)$

时域积分特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $\int_{-\infty}^{t}f(x)dx\leftrightarrow \pi F(0)\delta(\omega)+\frac{F(j\omega)}{j\omega}$

其中$F(0)=F(j\omega)|_{\omega=0}=\int_{-\infty}^{\infty}f(t)dt$

推论：

1. 若 $f’(t)\leftrightarrow F_1(j\omega)$

则 $f(t)\leftrightarrow \frac {F_1(j\omega)}{j\omega}+\pi[f(-\infty)+f(\infty)]\delta(\omega)$

1. 若 $f^{(n)}(t)\leftrightarrow F_n(j\omega)$且$f(-\infty)+f(\infty)=0$

则 $f(t)\leftrightarrow \frac {F_n(j\omega)}{(j\omega)^n}$

频域微分特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $(-jt)^nf(t)\leftrightarrow F^{(n)}(j\omega)$

频域积分特性

若 $f(t)\leftrightarrow F(j\omega)$

则 $\pi f(0)\delta(t)+\frac {f(t)}{-jt}\leftrightarrow \int_{-\infty}^{\omega}F(jx)dx$

其中$f(0)=\frac 1 {2\pi}\int_{-\infty}^{\infty}F(j\omega)d\omega$

卷积定理

若 $f_1(t)\leftrightarrow F_1(j\omega)$ $f_2(t)\leftrightarrow F_2(j\omega)$

则 $f_1(t)*f_2(t)\leftrightarrow F_1(j\omega)F_2(j\omega)$

若 $f_1(t)\leftrightarrow F_1(j\omega)$ $f_2(t)\leftrightarrow F_2(j\omega)$

则 $f_1(t)f_2(t)\leftrightarrow \frac 1 {2\pi}F_1(j\omega)*F_2(j\omega)$

相关定理

若 $f_1(t)\leftrightarrow F_1(j\omega)$ $f_2(t)\leftrightarrow F_2(j\omega)$

则$[R_{12}(\iota)]\leftrightarrow F_1(j\omega)F_2^*(j\omega)$

$[R_{21}(\iota)]\leftrightarrow F_1^*(j\omega)F_2(j\omega)$

10. 频谱

意义

表示信号的一种方法

定义

频谱 周期信号分解后 ，各分量的幅度和相位对于频率的变化，分别为幅度谱和相位谱。

频谱图 将幅度和相位分量用一定高度的直线表示

其中幅度谱图反映了信号不同频率分量的大小。

画图

先化简成系数为加号的，且均是cos的。坐标是{$A_n\to\omega$,$|F_n|\to\omega$,$\phi\to\omega$}

单边谱 与 双边谱 与 振幅频谱 与 相位频谱

$|F_n|$是$n$的偶函数，双边幅度谱的谱线高度为单边幅度谱的一半 ，且关于纵轴对称；而直流分量值不变 。

$\phi_n$是$n$的奇函数，双边相位谱可以由单边相位谱直接关于零点奇对称。

$F(j\omega)$幅度频谱，频率$\omega$的偶函数

$\phi(\omega)$相位频谱，频率ω的奇函数

频谱分类	直流分量	幅度	相位	n
单边谱	$\frac {A_0} 2$	$A_n$	$\phi_n$	$n=0,1,2,\dots$
双边谱	$F_0$	$	F_n	$	$\phi_n$	$n=0,\pm1,\pm2,\dots$
振幅频谱
相位频谱

注：

1. 若$F_n$为实数，那么可用$F_n$的正负来表示相位为$0$或者$\pi$，这时常把幅度谱和相位谱画在一张图上。
2. 既要画出单边谱又要画出双边谱；既要画出幅度谱又要画出相位谱

周期信号的频谱

周期信号的表达式

$f(t)=\sum_{n=-\infty}^{\infty}F_ne^{jn\Omega t}$

$F_n=\frac1T\int_{-\frac T2}^{\frac T 2}f(t)e^{-jn\Omega t}dt$

以矩形脉冲为例

• 基频 $\Omega$
  相邻谱线的间隔 $\Omega=\frac {2\pi}T$

  频带宽度（带宽） $B_f=\bigtriangleup F=\frac 1 \iota$ $B_\omega = \frac {2\pi}\iota$

  注 根据单位来判断用什么： $rad/s$ 还是 $s^{-1} 或者\ Hz$

  第一个零点 $\omega=\frac{2\pi}{\iota}$ $f=\frac 1 \iota$

  • 对于一般周期信号，将幅度下降为$\frac 1{10}|F_n|_{max}$区间定义为频带宽度。

  • 系统的通频带$>$信号的带宽，才能不失真。
    零点 $\omega=n\Omega=\frac{2m\pi}{\iota}$ $n=m\frac T \iota\ \ \ \ (m=\pm1,\pm2,\dots)$
    两零点间谱线间隔数 $\frac T \iota$

    相邻零点之间谱线数 $n=m\frac T \iota\ \ \ \ 谱线数为n-1或者n+1$

$F_n=\frac \iota TSa(\frac{n\Omega\iota}2)$

$f(t)=\displaystyle\sum_{n=-\infty}^{\infty}F_ne^{jn\Omega t}=\frac \iota T\sum_{n=-\infty}^{\infty} Sa(\frac{n\Omega\iota}2)e^{jn\Omega t}=\frac \iota T\sum_{n=-\infty}^{\infty} Sa(\frac{n\pi\iota}T)e^{jn\Omega t}$

特点

1. 离散性：以基频$\Omega$为间隔的若干离散谱线组成
2. 谐波性：谱线仅含有基频$\Omega$的整数倍分量
3. 收敛性：整体趋势减小。因此，信号的功率集中在低频段。

谱线结构与波形参数的关系

假设$T$不变，$\iota$ 变小

• 谱线间隔$\Omega$不变
• 幅度下降
• 零点右移，两零点间的谱线数目$\frac T \iota$增加
• 时域压缩，频域展宽

$\iota$不变，$T$增加

• 幅度下降
• 谱线间隔$\Omega$下降
• 频谱变密。

非周期信号的频谱

定义

$T$趋向于无穷

• 谱线间隔$\Omega$趋向于0
• 谱线幅度$F_n$趋向于0
• 周期信号的离散频谱过渡为非周期信号的连续频谱

频谱密度函数

虽然各频率分量的幅度趋近于无穷小 ，但无穷小量之间相对大小仍有差别，因此，引入频谱密度函数（单位频率上的频谱）。

$T->\infty$

$\Omega->d\omega$ 无穷小量

$n\Omega->\omega$ 离散$->$连续

$F(j\omega)=\displaystyle\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$ $F( j\omega)$称为$f(t)$的傅里叶变换

$f(t)=\frac 1{2\pi}\int_{-\infty}^{\infty}F(j\omega)e^{j\omega t}d\omega$ $f(t)$称为$F( j\omega)$的傅立叶逆变换

简记为： $f(t)\leftrightarrow F(j\omega)$

$F( j\omega)$一般是$F( j )$复函数，写为$F(j\omega)=|F(j\omega)|e^{j\phi(\omega)}$

$F(j\omega)\thicksim\omega$幅度频谱，频率$\omega$的偶函数

$\phi(\omega)\thicksim\omega$相位频谱，频率ω的奇函数

11.周期信号

周期信号的功率

$P=\frac1T\int_{-\frac T 2}^{\frac T 2}f^2(t)dtP=|F_0|^2+\displaystyle2\sum_{n=1}^{\infty}|F_n|^2=\displaystyle\sum_{n=-\infty}^{\infty}|F_n|^2=|F_0|^2+\frac 1 2A_n^2$

在时域中求得的信号功率与在频域 中求得的信号功率相等。

12. 功率信号 与 能量信号

• 能量信号 $E<\infty$ $P=0$
• 功率信号 $E=\infty$ $P<\infty$
• 时限信号是能量信号
• 周期信号、直流信号、阶跃信号是功率信号
• 非周期信号可能是能量信号，也可能是功率信号（$e^{j\omega t}$）
• 有些信号既不是能量信号也不是功率信号，如$f(t)=e^t$

其他

1. $a^k\epsilon(k )*\epsilon(k-4)$结果中应该用$\epsilon(k-4)$作为限定。
   . $\int_{t_1}^{t_2}f^2(t)dt=\displaystyle\sum_{j=1}^{\infty}C_j^2K_j$ 帕斯瓦尔方程

   其中$f(t)=C_1\phi_1(t)+C_2\phi_2(t)+\cdots+C_n\phi_n(t)=\displaystyle\sum_{j=1}^{n}C_j\phi_j(t)$

   $K_j=\frac T 2$

   因此有$P=\frac 1 T\int_{-\frac T 2}^{\frac T 2}f^2(t)dt=\frac 1 T\displaystyle\sum_{j=1}^{\infty}C_j^2K_j=\frac 1 2\sum_{j=1}^{\infty}C_j^2$

2. 三角函数在一个周期内的积分为0

3. $R_{12}(\iota)=f_1(t)*f_2(-t)$

4. 求零状态响应：

   • 离散 递推出$y_{zs}(0)\ \ \ \ y_zs(1)$ 其中，递推时的$y_{zs}(-1)=y_{zs}(-2)=0$
   • 连续 根据系数匹配原则求出$y_{zs}(0_+)\ \ \ \ \ y’_{zs}(0_+)$

5. 求零输入响应：

   • 离散 $y_{zi}(-1)=y(-1)$

     ​ $y_{zi}(-2)=y(-2)$

   • 连续 $y_{zi}^{(j)}(0_+)=y_{zi}^{(0)}(0_-)=y^{(j)}(0_-)$

信号与系统——公式篇

$\int_{-\infty}^{t} \epsilon(\iota) d\iota = t \epsilon(t)$

$x^2+Px+Q=0$

$a=-\frac P 2 $

$b=\frac{\sqrt{4Q-P^2}}{2}$

$x=a+jb=\rho e^{\pm j\beta}$

$\rho=\sqrt{a^2+b^2}$

$\beta=arcsin\frac b \rho$

$e^{jx}=cosx+jsinx$

$cosx=\frac{e^{jx}+e^{-jx}}2$

$sinx=\frac{e^{jx}-e^{-jx}}{2j}$

$ \delta (t) = \frac{d \epsilon(t)}{dt} $

冲激响应 $h(t)=\frac{dg(t)}{dt}$

$ \epsilon(t) = \int_{-\infty}^{t} \delta(\iota) d\iota $

阶跃响应 $ g(t)=\int_{-\infty}^th(\iota)d\iota$

所以：$ \epsilon(t-a) = \int_{-\infty}^{t-a} \delta(\iota) d\iota $

$\delta(k)=\epsilon(k)-\epsilon(k-1)$

$\epsilon(k)=\displaystyle\sum_{i=-\infty}^{k}\delta(i)$

$\epsilon(k)=\displaystyle\sum_{j=0}^\infty\delta(k-j)$

$ \int_{-\infty}^{\infty}f(t)\delta(t-a)dt=f(a) $ 冲激函数的取样性质

$\int_{-\infty}^{\infty}f(t)\delta^{(n)}(t)dt=(-1)^nf^{(n)}(0) $

$f(k)\delta(k-k_0)=f(k_0)\delta(k-k_0)$ 单位脉冲序列的取样性质

$\displaystyle\sum_{k=-\infty}^{\infty}f(k)\delta(k-k_0)=f(k_0)$

$\displaystyle\sum_{k=-\infty}^{\infty}\delta(k)=1$

$ f(t)\delta’(t)=f(0)\delta’(t)-f’(0)\delta(t)$

$ \delta^n(at)=\frac1{|a|}\frac1{a^n}\delta^n(t)$

$ \delta(at-t_0)=\frac1{|a|}\delta(t-\frac{t_0}{a})$

当$a=-1$ 的时候，$\delta(t)$为偶函数，而$\delta’(t)$为奇函数，注意$t_0$也需修改的

$\int_{-\infty}^{t}\delta’(t)dt=\delta(t)$ 注意上限为$t$而不是$\infty$

$y_{zs}(t)=f(t)*h(t)=\int_{-\infty}^{\infty}f(\iota)h(t-\iota)d\iota$

$y_{zs}(k)=f(k)*h(k)=\displaystyle\sum_{i=-\infty}^{\infty}f(i)h(k-i)$

$f(t)*\delta(t)=f(t)$

$f(k)*\delta(k)=f(k)$

$f(t)*\delta’(t)=f’(t)$

$f(t)*\epsilon(t)=\int_{-\infty}^tf(\iota)d\iota$

$f(k)*\epsilon(k)=\displaystyle\sum_{i=-\infty}^kf(i)$

$\epsilon(t)*\epsilon(t)=t\epsilon(t)$

$\epsilon(t)*\epsilon(t+a)=(t+a)\epsilon(t+a)$

$\epsilon(k)*\epsilon(k)=(k+1)\epsilon(k)$

$\frac{d^n}{dt^n}[f_1(t)f_2(t)]=\frac{d^nf_1(t)}{dt^n}f_2(t)=f_1(t)\frac{d^nf_2(t)}{dt^n}$ $\bigtriangledown[f_1(k)f_2(k)]=\bigtriangledown f_1(k)f_2(k)=f_1(k)\bigtriangledown f_2(k)$

$\int_{-\infty}^{t}[f_1(\iota)f2(\iota)d\iota]=[\int_{-\infty}^{t}f_1(\iota)d\iota]f_2(t)=f_1(t)*[\int_{-\infty}^{t}f_2(\iota)d\iota]$

当$f_1(-\infty)=0$或者$f_2^{(-1)}(-\infty)=0$下有： $f_1(t)f_2(t)=f_1’(t)f_2^{(-1)}(t)$

$e^{-at}\epsilon(t)*e^{-at}\epsilon(t)=te^{-at}\epsilon(t)$

$e^{-a_1t}\epsilon(t)*e^{-a_2t}\epsilon(t)=\frac 1{a_2-a_1}(e^{-a_1t}-e^{-a_2t})\epsilon(t) $ $ (a_1 \not= a_2)$

$f(t)\delta_T(t)=f(t)\displaystyle\sum_{m=-\infty}^{\infty}\delta(t-mT)=\sum_{-\infty}^{\infty}f(t-mT)$

梳状函数：周期为T的周期单位冲激函数序列

$R_{12}(\iota)=\int_{-\infty}^{\infty}f_1(t)f_2(t-\iota)dt=\int_{-\infty}^{\infty}f_1(t+\iota)f_2(t)dt=f_1(t)*f_2(-t)$

$R_{21}(\iota)=\int_{-\infty}^{\infty}f_1(t-\iota)f_2(t)dt=\int_{-\infty}^{\infty}f_1(t)f_2(t+\iota)dt$

$R_{12}(\iota)=R_{21}(-\iota)$

$R(\iota)=\int_{-\infty}^{\infty}f(t)f(t-\iota)dt=\int_{-\infty}^{\infty}f(t+\iota)f(t)dt$

$R(\iota)=R(-\iota)$

$P=\frac1T\int_{-\frac T 2}^{\frac T 2}f^2(t)dt=\displaystyle\sum_{n=-\infty}^{\infty}|F_n|^2$

$P=|F_0|^2+\displaystyle2\sum_{n=1}^{\infty}|F_n|^2$

$P=|F_0|^2+\frac 1 2A_n^2$

$a_n=\frac 2 T\int_{-\frac T 2}^{\frac T 2}f(t)cos(n\Omega t)dt$

$b_n=\frac 2 T\int_{-\frac T 2}^{\frac T 2}f(t)sin(n\Omega t)dt$

$F_n=\frac1T\int_{-\frac T2}^{\frac T 2}f(t)e^{-jn\Omega t}dt$

$F(j\omega)=\displaystyle\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$

$|F_n|=|F_{-n}|=\frac12A_n$

转载请注明出处，谢谢。

愿 我是你的小太阳